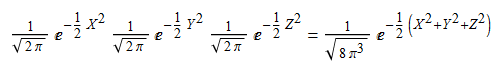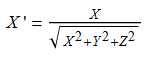Complex Projective 4-Space

The Platonic solids can be regarded as regular tilings of the surface of a sphere in much the same way as the square, hexagonal and triangular tilings of the plane are regular. For example, the dodecahedron is a tiling of the sphere with twelve pentagons.

If you read the ‘Projective geometry‘ chapter of MODA, you will see that the points on the projective plane can be identified with the lines through the origin or, equivalently, pairs of antipodal points on a sphere. So, we can identify opposite points on our dodecahedron as being ‘the same thing’. An advantage of this is that the visible half of the dodecahedron is the entire tiling of the projective plane:

This has 6 faces, 10 vertices and 15 edges, compared with the dodecahedron’s 12, 20 and 30, respectively. Hence, this tiling of the projective plane is called the hemi-dodecahedron. If we form the vertex/edge graph of the hemi-dodecahedron, the result is the rather famous Petersen graph:

Even though it can be drawn on the projective plane, it cannot be realised on the plane without edges crossing (as above). This is because it contains the complete graph K5 as a graph minor. The Petersen graph is really interesting in its own right, with Donald Knuth commenting that it is almost always a counter-example to false conjectures about graphs!

Returning to projective polyhedra, we can also construct its dual, the hemi-icosahedron. It is a remarkable fact that 11 hemi-icosahedra can be stitched together to form an abstract self-dual polytope, and likewise 57 hemi-dodecahedra constitute the 57-cell. In the same vein as the Rubik’s 120-cell mentioned earlier, Nan Ma recently designed a web applet for exploring a Rubik’s 11-cell. As far as I know, the same hasn’t yet been done for the 57-cell.

Quickly reading the Planar graphs section of Combinatorics II (third chapter of MODA), you’ll see how certain tilings such as the Klein quartic can be obtained by ‘rolling up’ finite patches of infinite tilings. The 11-cell and 57-cell are rolled up patches of the icosahedral and dodecahedral honeycombs, respectively. Claudio Rocchini rendered a really pretty stereographic projection of the former:

Hyperbolic honeycombs are the three-dimensional cousins of the tilings used in the Circle Limit paintings. Instead of the infinite variety in two dimensions, however, there are only four regular hyperbolic honeycombs.

Emma McCaughan notified me that topic of the 2012 Larmor Lecture organised by the Cambridge Philosophical Society is the Antikythera mechanism. It takes place at 5:30 pm today (Monday 8th October) in the Bristol-Myers Squibb lecture theatre, located on Lensfield Road (south of Downing College, Cambridge). It’s open to everyone and I’ll almost definitely be there.

Perhaps now would be a good time to mention that my demonstration is now online for you to mess around with. You can set the date and time to observe certain astronomical events. For example, you can enter the date of the 1999 solar eclipse (the only eclipse I’ve observed, as far as I can remember) and press the ominous ‘go to date’ button:

It’s pretty accurate, in that the Sun, Moon and Earth are collinear as expected. You can use this to see into the future as well. It’s based on Ancient Greek approximations to astronomical cycles, so loses accuracy when you start to go too far away from the present.

If/when I understand completely the Freeth-Jones model (hopefully today’s lecture will shed some light), I’ll make an updated version of this demonstration to indicate planetary motions. The model has a similar pin-and-groove system to the lunar display to emulate the elliptical orbits of each planet, but I don’t yet know the exact tooth counts.

If you lived somewhere other than Britain, you may have been one of the lucky people to observe the recent Transit of Venus. Otherwise, you’ll have to either wait for the updated demonstration or view it in Stellarium. Still, nothing can compare to watching the real thing; I hope Ray Kurzweil can extend my life so I can observe the next one (2117).

See you in 2.5 hours!

Dating the discovery of the integers is difficult indeed. Positive integers have been used since time immemorial for counting, and positive rationals were later used by the Ancient Greeks to express lengths. However, this was not sufficient, as the Pythagorean theorem shows that the diagonal of a unit square is irrational. Someone was even drowned for proving this! Is he really to blame for the existence of irrational numbers? Anyway, we need a larger field of numbers, the reals, to account for this.

John Conway developed a much larger ordered field, encompassing Cantor’s infinite ordinals as well. We’ll explore this idea in the environment of combinatorial game theory. Lots of games can be associated with surreal numbers; one of the simplest is the game of Hackenbush mentioned in a book by Conway, Guy and Berlekamp.

Rules

The state of the game is represented by a tree, the edges of which are either violet or green. One vertex of the tree is identified as the ‘root’ (coloured black in these examples). For instance, the following is a valid position in Hackenbush:

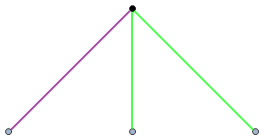
Alice and Bob have opted out of being used as example names on Complex Projective 4-Space, so I’ll instead have to resort to using names of people who particularly enjoy the site.

• Vishal and Gabriel alternate turns removing edges: Vishal can only remove violet edges, whereas Gabriel can only remove green edges.
• Some parts of the graph may end up ‘cut off’ from the root in the process. Rather like pruned branches of a plant, they immediately die and disappear.
• This process continues. A player loses when he or she has no valid move.

Evaluating games

A game is described as positive if Gabriel can force a win, negative if Vishal can force a win, or zero if the person who goes first loses. Clearly, in this instance, it is a win for Gabriel, so the game is positive. Indeed, this game is associated with the number +1. Another equivalent game is shown below, also with a value of +1:

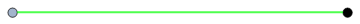
In order to calculate the values of various games, we’ll use some axioms:

1. If two games a and b are welded together at the root vertex to form a third game, it has value a + b.
2. If all colours are inverted in a game c, we obtain the game −c.

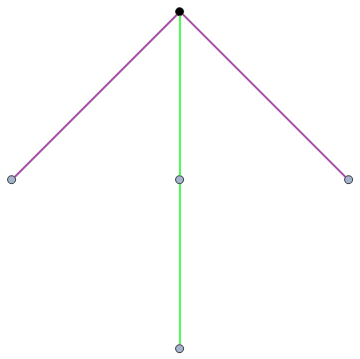
By axiom 2, the following game has value -1:

Vishal obviously wins irrespective of who goes first, as he can remove the violet edge, so this is indeed a negative game. We can add the previous two games together by fusing them at the roots to form a zero game, where the second player has a winning strategy:

So far, the games have been reasonably simple, as we have only considered star graphs (where the root is connected to all other vertices). What about the following game? What is its value?

Vishal and Gabriel each have two edges to remove, and neither of them can force their opponents’ edges to disappear. So, this game must again have value zero. By subtracting the violet edges, we obtain a game of value +2. This generalises in the obvious way; for instance, this game has value +4:

More complicated games include the one below. We don’t know what its value is yet, so we’ll call it x.

This must be negative, as Vishal wins. It looks more positive than -1, though, since Gabriel still has a green edge he can remove. We can deduce the value of x by using our axioms. Consider the following tree:

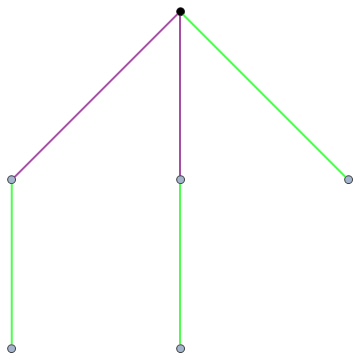
Try playing this with a friend. You should find that, no matter which colour you are, the second player wins. So, this game has value 0, and we can deduce that 2x + 1 = 0. In other words, the original game has value -1/2. We can access any dyadic rational using a finite string, such as -25/16:

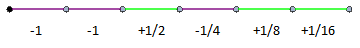
Bigger trees than Sequoia sempervirens

By allowing infinite trees, further numbers can be accessed. We can obtain any real number, for example, by utilising its binary expansion. We can also obtain the infinite ordinal ω (a green string of infinite length), and the infinitesimal ε (shown below).

We can go further by using Cantor’s infinite ordinals to express positions of vertices, and create even bigger infinities and infinitesimals. For instance, we can have a generalised string with value 2ω:

We can verify that this is indeed the case, as Vishal would need two infinite rooted strings of violet edges to restore this to a balanced (zero) game. We can get things that aren’t even ordinals in the traditional sense, such as the game ω − 1:

This effectively constructs the tree of Conway’s surreal numbers. Going down-left on the tree corresponds to appending a violet edge to the end of a string, whereas going down-right corresponds to appending a green edge. Lukas Lansky drew this tree for the Wikipedia article on surreal numbers:

http://en.wikipedia.org/w/index.php?title=File:Surreal_number_tree.svg&page=1

Arithmetic with (generalised) surreals

Surreal numbers can be recursively added, subtracted, multiplied and divided, just like real numbers. We say they form an (ordered) field. Indeed, they constitute the absolute largest possible ordered field.

If you were under the impression that this is completely crazy, things are going to get a lot worse. The surcomplex numbers are of the form a + ib, where a and b are surreal numbers and i is the imaginary unit. Like the complex numbers, they are algebraically complete: any polynomial equation in the surcomplexes can be solved.

As the Cayley-Dickson construction depends only on defining addition and multiplication, we can obtain surquaternions (non-commutative!), suroctonions (non-associative!) and, worst of all, sursedenions. I wouldn’t be surprised if there’s a generalisation of this blog with infinite posts, namely Surcomplex Projective 4-Space!

If I were more diligent and could actually be bothered to tag and categorise my blog posts, this one would belong in the esoteric realm of ‘probabilistic geometry’.

Suppose we have three variables, X, Y and Z, which are independent and random, determined by the bog-standard normal distribution with mean 0 and variance 1. The probability distribution function of each variable looks something like this:

I encountered a puzzle somewhere, where you have to obtain a uniform random distribution just by applying basic operations to these three variables. A uniform distribution looks like this:

How, then, is it possible to convert something as smooth and curvaceous as the normal distribution into a discrete and discontinuous uniform distribution? Surely it’s impossible? You may want to have a go at it yourself before I reveal all.

Somewhat surprisingly, we can indeed solve the puzzle by using a theorem of Archimedes. When a sphere is inscribed in a cylinder, and an arbitrary horizontal ‘slice’ is taken, the curved surface areas of the sphere and cylinder are identical:

The Archimedean map projection involves projecting the surface of the Earth (assumed to be a sphere) onto a circumscribing cylinder. By Archimedes’ theorem, areas are preserved in this matter. The sphere can then be unrolled out to form a flat map. Usually, however, people use the Mercator projection instead, which preserves angles instead of areas. You may recognise angle-preserving (conformal) maps from Escher’s Circle Limit pictures.

Returning to the original problem, we can view each of X, Y and Z as axes in three-dimensional space and obtain a three-dimensional probability density function. This is the product of the probability density functions of the three original variables:

Since it depends only on X^2+Y^2+Z^2, the squared distance from the origin, it must therefore have spherical symmetry. We can thus obtain a uniform distribution over the surface of the unit sphere by ‘normalising’ X, Y and Z to ensure that the squared distance from the origin is 1.

If we let the x-axis be the axis of the cylinder, applying the Archimedean projection will not affect the value of X’. Since all slices of a cylinder are identical, X’ must therefore be uniformly distributed over the interval [-1,1]. Success!

I’ll end on another puzzle, introduced to me by Geoff Smith. I can’t recall the exact wording of the original statement of the problem, so I’ll improvise:

Deep within the Arctic Circle, a group of elves were busy making mathematical puzzles to deliver to children on Christmas Day. Unfortunately, there was a hole in the Arctic ice of diameter one metre, and they were worried that one of Geoff’s reindeer may fall into the tundra and perish. Hence, in the interests of ‘elf and safety*, it had to be covered with wooden planks. Obviously, we can use parallel planks (with a combined width of one metre) to cover it. Is it possible to have a combined width less than one metre if we adopt an intricate criss-crossing structure instead?

* Pun-believable joke conceived by Andrew Carlotti.

I shall be rather busy during the next couple of months, so there may be a noticeable drop in the frequency of posts on Complex Projective 4-Space. Nevertheless, I shall endeavour to maintain a steady stream of interesting articles, assuming I have time to do so.

Puzzle

In the meantime, here is a puzzle Dan Asimov discovered in an obscure journal: Find a set of n distinct points on the Euclidean plane, such that the perpendicular bisector of any pair of points passes through exactly two points in the set. I rediscovered the same solution as in the journal, and we believe that this is the unique solution up to similarity. I’ll not post any spoilers yet.

Rhombic ruminations

I’ll start by explaining the title of this section. The word ‘ruminations’ can refer to deep contemplations, and also to the process by which a ruminant re-digests its food.

In the world of golden rhombi, Christian Perfect constructed a couple of Wieringa roofs at the Newcastle MathsJam following my instructions. His first attempt ended up exhibiting too much positive curvature, but made a decent hat:

Tessellations of [non]-Euclidean space

Tim Hutton and I are experimenting with different honeycombs for the program Ready. He implemented the triakis truncated tetrahedral tiling recently, and created a couple of Wikipedia pages related to it. You may recognise it as the Voronoi diagram of atoms in a diamond.

We’re also trying out non-Euclidean tessellations. Analogous to the BCC lattice of truncated octahedra in Euclidean 3-space, there is a hyperbolic tiling of truncated icosahedra. There was some discussion about this fifteen years ago. One proof of its existence is its Coxeter-Dynkin diagram, relating it to a known hyperbolic tessellation.

We’ll begin by considering Hamiltonian quaternions, a four-dimensional extension to the complex numbers. A particularly interesting bunch of quaternions is the multiplicative group of 120 ‘icosians’. These can be thought of as the vertices of a 600-cell or, by duality, the centres of the dodecahedra in the 120-cell. The simplest icosian is, without a doubt, 1. Let’s centre a single dodecahedron at 1:

This dodecahedron appears slightly irregular, as I have used a stereographic projection to ‘unravel’ the curved surface of the 120-cell into flat Euclidean 3-space. We’ll consider another icosian quaternion, τ, with the value ½(φ + (1/φ)i + 0j + k). It still has unit length, same as the other 119 icosians, and is quite close to 1. The dodecahedron associated with this icosian is adjacent to the previous dodecahedron:

Proceeding logically, we draw dodecahedra at τ^2, τ^3 and so on. As τ^10 = 1, we obtain a closed loop of ten dodecahedra:

We can multiply the centres of the dodecahedra by another icosian to obtain another ring of dodecahedra. Since they are both great circles, and disjoint from each other, the only possibility is that they are entwined around each other. This is indeed the case:

We can repeat this process to obtain more linked rings. Whilst not the typical Olympic Games logo, or indeed the EGMO emblem, here are five linked rings forming a hollow torus capable of accommodating a sixth ring:

By symmetry, each ring in the 120-cell is surrounded by five others, and there are twelve in total. The other structure with this property is the dodecahedron itself: there are twelve pentagons, each of which is surrounded by five others. Is there an explanation for this curiosity?

The Hopf fibration is a bijection between the points on a sphere and a set of intertwining great circles on the surface of a hypersphere. The 120-cell is a tiling of the hypersphere by dodecahedrons just as the dodecahedron is a tiling of the sphere by pentagons. In other words, the interlocking rings of dodecahedra form a discrete Hopf fibration! Similar discrete Hopf fibrations are summarised below:

• 120-cell ↔ dodecahedron
• 24-cell ↔ tetrahedron
• tesseract ↔ dihedron

The dihedron, by the way, is the partitioning of the sphere into two hemispheres. It’s really boring, trivial and degenerate compared with the other regular spherical tilings, the Platonic solids.