Complex Projective 4-Space

Breaking news: Following the selection process at Oundle, the UK IMO team has now been selected. It comprises Gabriel Gendler, Frank Han, Freddie Illingworth, Warren Li, Harvey Yau and Joe Benton. It is very worrying that two of these people belonged to the same Balkan Mathematical Olympiad team responsible for a non-LaTeXed report!

Anyway, a particularly useful mathematical coincidence, first observed by Newton, is that the shape assumed by the surface of a rotating container of liquid is precisely the shape necessary to focus parallel light to a single point. It is a rather elementary exercise to prove this, and amazingly does not require the use of calculus.

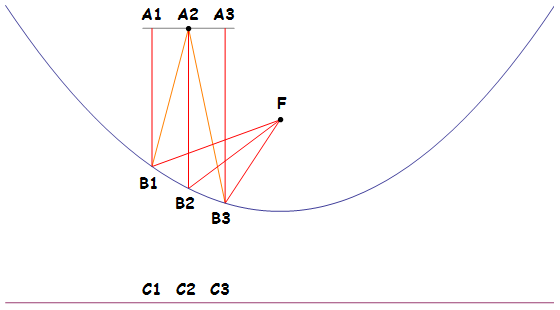
Theorem 1 (Archimedes): Light incident on a parabola from a direction perpendicular to its directrix is reflected to the focus.

Proof: Consider a light beam originating at A2 and travelling to F in the following diagram. We wish to show that the path A2 — B2 — F is shorter than any of the alternative paths, such as A2 — B1 — F and A2 — B3 — F, as then we would win by Fermat’s principle that light travels from source to destination in least* time over all such paths.

Recall that a parabola is defined to be the set of points that are equidistant from the focus and directrix. In other words, d(F, B1) = d(B1, C1), d(F, B2) = d(B2, C2), and d(F, B3) = d(B3, C3), where d(X, Y) denotes the distance between points X and Y. Also, observe that d(A1, C1) = d(A2, C2) = d(A3, C3), since these are just parallel lines of the same length. Consequently, we obtain the following result:

• The red rays are all of the same length.

Together with the fact that d(A2, B1) > d(A1, B1) and d(A2, B3) > d(A3, B3), this means that the path A2 — B2 — F is indeed shorter than the alternative paths. Q. E. D.

* Technically, it follows a path such that the time functional is stationary with respect to small variations in the path. This may be a maximum or saddle point rather than a (local) minimum, but this is rare.

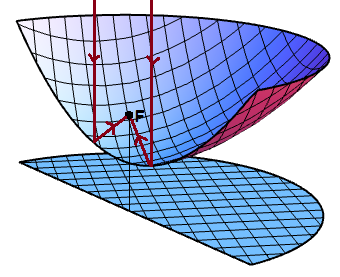
Corollary 2: Light perpendicular to the directrix incident upon a paraboloid is reflected to the focus.

Proof: Just take the two-dimensional slice containing the ray of light and the focus, then apply Theorem 1.

This proof is legitimate, as we know that the light ray must remain in this plane by the symmetry of the configuration.

Corollary 3 (Newton): It is possible to build a telescope using a paraboloid mirror.

Proof: You can buy one from Celestron.

Theorem 4 (Newton): Neglecting surface tension, the surface of a fluid in a container rotating at uniform angular speed about a vertical axis assumes the shape of a paraboloid.

Proof: Operate in the reference frame of the rotating container. Due to fluid friction (viscosity), the fluid will eventually become stationary, so u = 0 everywhere. Recall that the Navier-Stokes equation is:

Since u = 0, most things vanish and we are left with −∇p/ρ + ω²r e_r − g e_z = 0, where r is the distance from the axis of rotation and g is the acceleration due to gravity, and the things in bold are unit vectors. The last expression can be expressed as a gradient of a scalar potential, leading to the following equation:

• ∇(p/ρ − ½ω²r² + gz) = 0

Consequently, p/ρ − ½ω²r² + gz is constant throughout the fluid, including on the surface. Moreover, p is equal to the atmospheric pressure on the surface, so − ½ω²r² + gz is constant. This is the equation of a paraboloid with focal length g/2ω².

Newton realised that it is thus possible to build a telescope by using a container of reflective fluid rotated at constant speed. Unfortunately, maintaining a constant speed of rotation was prohibitively difficult, so he settled for hand-grinding a spherical mirror instead (spheres and paraboloids agree to quadratic order, which was good enough).

Nevertheless, liquid mirror telescopes now exist, the largest being the six-metre Large Zenith Telescope (so called because it points directly upwards). This has a parabolic mirror made from liquid mercury rotating at an angular speed of ω = 0.700 to maintain a focal length of 10.00 metres.

What about surface tension?

We have neglected surface tension in the derivation. Surface tension makes the surface of the liquid slightly more spherical, since a sphere has constant mean curvature whereas a paraboloid does not. The contribution from surface tension, however, is so minuscule that this doesn’t matter whatsoever.

A more important drawback is that the mirror can only point upwards, in the opposite direction to gravity. There are at least three ways to circumvent this:

• Use a space telescope with artificial gravity induced by rotation about another axis. No explicit examples have been constructed.
• Allow the liquid to solidify whilst being rotated. The result is a solid parabolic mirror. I was reading the new book that Alex Bellos sent me, entitled Alex Through the Looking Glass, which mentions that the Large Binocular Telescope was constructed using this method. Unfortunately, it is still required to correct the mirror by a slight amount of grinding (typically by sand-blasting with ions instead of sand).
• Use a large planar mirror, which is cheaper to construct than a curved mirror, to reflect light onto the paraboloid.

Here’s a metaphorical meteor shower of recent news worth mentioning:

1. The meteor shower associated with the debris of the 209P/LINEAR comet peaked in intensity last night. Apparently it wasn’t as impressive as anticipated.
2. Alexey Nigin has discovered a 12-face golyhedron. I suspect that this is most probably optimal.
3. The final selection process for the UK IMO team has just commenced. This year, the competition is more intense on the basis that there are ten contenders (instead of the usual eight or nine) for the six available positions.
4. Ray Goldstein et al have been investigating the dynamics of soap films under the deformation of the boundary.

Firstly, the results for the Balkan Mathematical Olympiad have been published. Consequently, the preliminary UK IMO squad is now larger than ever before, comprising ten people (six team members and four reserves, in some indeterminate order).

You are probably aware of the game of Noughts and Crosses (alternatively referred to as tic-tac-toe), in which one attempts to seize three collinear squares whilst attempting to prevent one’s opponent from doing likewise. What is less well-known, albeit mentioned in the Royal Institution Christmas Lectures several years ago, is that it’s entirely equivalent to the following problem:

We begin with the numbers {1, 2, 3, … 9}. Players alternate turns, taking an available (unclaimed) number. The first player to obtain three numbers which sum to 15 is declared the winner.

To demonstrate their equivalence, it suffices to show that we can label the squares from 1 to 9, inclusive, such that every sum to 15 corresponds to a unique line, and vice-versa. This is accomplished by the following magic square:

It is immediate from the definition of the magic square that all lines (sets of three collinear squares) consist of three distinct numbers in the range {1, 2, …, 9} summing to 15. What is less obvious is the converse, that every such set is represented by a line. I only just realised the real reason behind this, which hitherto seemed to be a mere coincidence. Firstly, we decrement each of the numbers by 5, so that all line sums are zero.

Now, think of these as points rather than squares. For convenience, we shall allow 0 to be the origin. On the diagram below are the curves x(x − 1)(x + 1) = 0, y(y − 1)(y + 1) = 0, and the linear combination x(x − 1)(x + 1) = 2y(y − 1)(y + 1). The latter must also pass through all nine grid points, being a combination of the other two.

This is an elliptic curve, so it admits a well-known Abelian group structure. We chose the coefficient 2 in the equation for the curve specifically so that the tangent at -1 intersects the elliptic curve again at 2; similarly, the tangent at -2 intersects the curve again at 4. From this and the remaining lines, it is easy to see that the elliptic curve group operation corresponds to ordinary integer addition. And we know that three points on an elliptic curve sum to zero if and only if they are collinear (c.f. my elliptic curve calculator, which was recently made into a video by James Grime of DAMTP):

[youtube=http://www.youtube.com/watch?v=LWkOkM0Gqa4]

Anyway, generalising this idea, we can show that the following two games are equivalent:

• Generalised Noughts and Crosses, where the squares are positioned at non-torsion points on an elliptic curve and you win with three collinear copies of your symbol;
• A game in which you and your opponent alternate taking numbers from a predetermined set, and attempt to obtain three numbers summing to a predetermined total.

By looking through the Elliptic Curves on a Small Lattice, I found a game of Generalised Noughts and Crosses on a reasonably small grid corresponding to the game where you attempt to form a total of 27 from three numbers in the range {1, 2, 3, …, 17}:

You can verify for yourself that sets of three collinear squares are in bijective correspondence with sets of three numbers in the range {1, 2, …, 17} summing to 27.

A most delightful way to procrastinate is to attempt the unsolved problems on MathOverflow. Especially rewarding is when you actually end up solving such a problem, or when you learn something in the process, or both. Last night I learnt the terms golygon (coined by Lee Sallows) and golyhedron (coined by Joseph O’Rourke before their existence had even been established), eventually providing an example of the latter after a reasonable amount of work.

Golygons

A golygon is a lattice polygon where all angles are right-angles, and the sides have consecutive integer lengths {1, 2, 3, …, n}. The simplest example is the following octagon:

Notice that the edges, in cyclic order, are {1, 2, 3, 4, 5, 6, 7, 8}. The Wikipedia article mentions the interesting fact that this is capable of tiling the plane, and indeed this is possible: two copies of the tile, rotated 180°, can be slotted together to form a unit cell which can tessellate the plane periodically.

One problem is to count the number of golygons with n edges. If we allow self-intersections, then this amounts to counting the number of solutions to the following equations:

• ± 1 ± 3 ± 5 ± … ± (n − 1) = 0
• ± 2 ± 4 ± 6 ± … ± n = 0

Obviously, n must be even, since we alternate between vertical and horizontal moves. We also require 2 + 4 + 6 + … + n to be a multiple of 4, so as to be able to partition it into two sums of even numbers; this means that n is congruent to either 6 or 0 (modulo 8). Finally, we require 1 + 3 + 5 + … + (n − 1) to be even, so n must be divisible by 4. Consequently, every golygon has n = 8k edges for some positive integer k. These are enumerated by this sequence, which uses generating functions.

Forbidding self-intersections makes the problem much harder, as we are then counting self-avoiding walks of a particular nature. This problem is, in general, very difficult.

Golyhedra

This was, of course, merely a warm-up for explaining the three-dimensional generalisation, a golyhedron. In defining a golyhedron, Joseph O’Rourke first imposed some suitable regularity conditions:

• All vertices of P belong to the three-dimensional integer lattice ;
• All edges of P are parallel to a coordinate axis;
• All faces of P are simply-connected;
• The boundary ∂P is topologically a sphere.

‘Regularity conditions’ just mean that we restrict attention to objects that are quite nice. For example, in differential geometry one considers surfaces that are continuously differentiable; in complex analysis, we mostly consider holomorphic functions on open subsets of the complex plane (or some other Riemann surface).

Naturally, we still have to impose a further condition, namely the interesting one. The area sequence of P is the sorted list of the areas of the faces of P. He proceeds to give a very helpful example:

If we did this for the golygon at the beginning of the page, and modified the definitions to apply to two-dimensional polygons, then it would have a length sequence of {1, 2, 3, 4, 5, 6, 7, 8}. This motivates the definition of a golyhedron:

• A golyhedron is a polyhedron P obeying the four aforementioned regularity conditions and possessing area sequence {1, 2, 3, … , n} for some n.

After some experimentation, Joseph O’Rourke conjectured that no such golyhedra exist. It is difficult, for example, to avoid having lots of faces with small area. Somewhat out of the blue, I was inspired by this orthogonal polyhedron from David Eppstein’s blog post.

Eppstein mainly focused on the skeleton of the polyhedron, which is a vertex-transitive 3-regular graph with 24 vertices and 36 edges. However, for this problem we are more interested in the faces of the polyhedron, of which there are twelve. They are all L-shaped, and come in pairs whose areas differ by 2.

Obviously, this toroidal polyhedron fails for multiple reasons. Firstly, its surface is not topologically a sphere. Secondly, it is far from being a golyhedron, since the symmetry means that areas are repeated. However, it seemed quite promising, since it might be possible to realise a golyhedron using a similar local structure. In particular, I envisaged something like this:

Ignore, for the moment, the fact that this actually is a golyhedron. It is simply-connected, and principally consists of a long tortuous chain of unit cubes, which changes direction like so:

down, left, forwards, up, right, backwards, down, left, forwards, up, right, backwards

This cycles through the directions in the same way as Eppstein’s doughnut, so we end up with a bunch of L-shaped faces occurring in pairs whose areas differ by 2. If we simply truncated the ends of the chain, we would have two faces of area 1, so I instead terminated the ends with club-foot constructions.

I decided that it would be helpful to build the club-feet first, and then attempt to connect them together using a chain. Note that the opposite L-shapes have areas differing by 2, so I needed the areas unused by the club feet to be partitionable into pairs of that form. I also wanted the club feet to include the faces of small area, so that the L-shapes could be nice and large. Subject to these constraints, I found the following possible sequence:

The 14 red numbers are those covered by the club feet. The remaining 18 black numbers can be matched into 9 pairs as shown above; these will be represented by pairs of L-shapes. We will define the abstract length of an edge in the chain to be n − 1, where n is the number of cubes. Then the L-shapes induced by consecutive edges of length n and m will have areas of n + m ± 1. Consequently, we obtain the following system of equations:

• 1 + a = x1
• a + b = x2
• b + c = x3
• c + d = x4
• d + e = x5
• e + f = x6
• f + g = x7
• g + h = x8
• h + 5 = x9

where all of the variables are positive integers, and {x1, …, x9} are (in some order) {8, 12, 15, 16, 19, 22, 23, 26, 27}. By subtracting the even-indexed xs from the odd-indexed xs, we obtain:

• x1 − x2 + x3 − x4 + x5 − x6 + x7 − x8 + x9 = 6

And of course, the sum of the xs is equal to the sum of {8, 12, 15, 16, 19, 22, 23, 26, 27} (the mean values of each pair), namely 168, giving another linear equation:

• x1 + x2 + x3 + x4 + x5 + x6 + x7 + x8 + x9 = 168

A change of basis gives these two simpler equations:

• x1 + x3 + x5 + x7 + x9 = 87
• x2 + x4 + x6 + x8 = 81

A possible solution to this is the partition {8, 15, 19, 22, 23} ∪ {12, 16, 26, 27}. We then need to choose the order of the terms within each part to accomplish each of the following goals:

• a, b, …, h are all positive;
• The resulting polyhedron does not self-intersect.

After experimentation, I settled on the order (8, 12, 15, 26, 19, 16, 22, 27, 23) for the xs, which gives edge lengths (a, b, …, h) = (7, 5, 10, 16, 3, 13, 9, 18). The resulting golyhedron is shown below:

So, we have a golyhedron with 32 faces. What is the smallest number of faces possible?

Any golyhedron must have an even surface area, so the number of faces must be congruent to either 0 or 3 (modulo 4). There are also no 7- or 8-faced golyhedra, since any such polyhedron must (by the pigeonhole principle) have a plane (either xy, yz or zx), parallel to which there are only two faces, which must therefore both have equal area.

Consequently, we can bound the minimum number of faces of a golyhedron between 11 and 32. Can you improve upon those bounds?

If so, either comment here or (if you have a MO account) the original question.

Whilst submerged beneath several blankets in my morning hypnopompia, I was awakened by the Today programme on Radio 4. Specifically, I heard news that the Pet Shop Boys are due to perform an orchestral biography of the mathematician and cryptanalyst Alan Turing at the BBC Proms.

Being a massive fan of both Alan Turing and the Pet Shop Boys (I should have been born two decades earlier), I decided to relieve the Aperiodical of reporting another story about Alan Turing by instead mentioning it here.

Based on what I gathered from listening to the radio whilst half-asleep, the composition is inspired by sections of Andrew Hodges’ autobiography Alan Turing: The Enigma. I seem to recall that this included the Pet Shop Boys singing ‘in Cambridge’ (to the tune of their earlier single, In Suburbia) and ‘universal machine’ amongst other lyrics.

Apparently the Proms will begin on the 18th July in the Royal Albert Hall, so ensure you tune in for the Turing opus.

In the 1994 proceedings of the Mathematical Association of America, there is a truly wonderful article by Jonathan King. Entitled Three Problems in Search of a Measure, it provides three very different examples of problems that can be solved using elementary methods by considering the notion of a measure. The appeal of the article stems largely from the fact that the proofs are so clean and elegant, motivating measures and ergodic theory without having to rely on any advanced theorems.

One of the problems is the Arctic circle problem, which I first encountered in Geoff Smith’s Geometry Thoughts for the Day on 2011-06-11:

This problem is quite well known, and is related to something that has been discussed recently. A fishing hole in the ice forms a perfect circle of diameter d. A rich supply of arbitrarily thin planks of all sorts of length and widths is available. The hole must be covered with planks for Health ‘n Safety. Clearly this can be done with a finite collection of planks of total width d by placing them in parallel fashion.

Is it possible to cover the hole by using a finite collection of planks of total width less than d by using some kind of cunning criss-cross arrangement of the planks?

I’ll leave you to contemplate this; it’s very satisfying to solve.

Poncelet’s porism

Suppose we have an n-gon with both an incircle and a circumcircle. Poncelet’s porism is the theorem that we can then find infinitely many n-gons sharing the same incircle and circumcircle, by starting from any point on the circumcircle. If you prefer, Wolfram MathWorld has a very instructive animation of the statement of the porism:

The usual ‘proof from the book’ of Poncelet’s porism involves the theory of elliptic curves. By comparison, the concepts in King’s proof are sufficiently elementary that I claim the proof could be understood by the Ancient Greeks. To emphasise this point, I shall present a slight reworking of King’s proof as a Socratic dialogue between Archimedes (who has hypothetically discovered the proof) and Eratosthenes. I have chosen Eratosthenes over the more usual candidates of:

• Meno’s slave (if you’re Plato);
• A Magdalene undegraduate reading Land Economy through the bottom of a Pimm’s glass (if you’re Piers Bursill-Hall);
• Tim Gowers’s son (if you’re Tim Gowers);

on the basis that I wanted a contemporary of Archimedes who would be able to understand the subtleties of the proof.

Quod erat demonstrandum. By the way, the result can be generalised to ellipses instead of circles by applying a projective transformation, although of course this would be beyond Ancient Greek mathematics so I decided against including it in the Socratic dialogue.