Complex Projective 4-Space

You are probably aware of classical logic gates, such as the Boolean AND and OR gates. The input(s) and output(s) of a logic gate take values in the set {0, 1}, usually identified with ‘false’ and ‘true’, respectively.

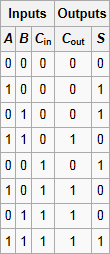
One example with multiple inputs and outputs is the full adder, so called because of its ability to perform binary addition, which has three inputs (A, B, C) and two outputs (S, C’). It can be represented by a truth table, which gives the values of S and C’ given any combination of A, B, C:

Thinking of this as a function from {0, 1}^3 to {0, 1}^2, we can also represent this as a binary matrix with eight columns and four rows, where every column contains a single ‘1’. This matrix is particularly interesting when it is a permutation matrix, corresponding to a bijective function. (Of course, this is only possible when the logic gate has equally many inputs and outputs.) These logic gates are known as reversible logic gates. It is a remarkable fact that reversible gates can perform any classical computation, and that there is a three-input universal gate, namely the Fredkin gate. This has three inputs, A, B and C, and three outputs, A’, B’, C’, with the following definition:

(A’, B’, C’) = (A, B, C) if C = 0, and (A’, B’, C’) = (B, A, C) if C = 1.

Anyway, if we generalise the definition of a logic gate to include any unitary matrix, rather than merely permutation matrices, then we obtain logic gates capable of creating a quantum superposition of outputs. For instance, the Hadamard gate has one input and one output, and corresponds to the following matrix:

Another example is the controlled phase gate, which is a diagonal matrix with entries . Conditional on the first qubit (quantum bit) being in state |1›, this rotates the Bloch sphere (space of possible states, which is isomorphic to the complex projective line or Riemann sphere) of the second qubit. It was used by Peter Shor to construct a circuit of logic gates capable of applying the quantum Fourier transform.

Quantum computing

The primary interest in quantum logic gates derives from the fact that they can actually be implemented as physical systems, relying on quantum-mechanical phenomena such as quantum entanglement and the ability for the system to occupy a superposition of states. Certain problems have known solutions in probabilistic polynomial time with quantum computing, but no known probabilistic polynomial time solutions with classical computing. These include the problems of integer factorisation, discrete logarithm and its counterpart over elliptic curves. All of these are solved in cubic time by Shor’s algorithm.

At the moment, quantum computing is still very much in its infancy. Shor’s algorithm has indeed been implemented, but the largest number to be factored in this way was 21 (until recently, the record was 15). As technology improves, quantum computers executing Shor’s algorithm could considerably compromise RSA cryptography and elliptic curve cryptography. Indeed, I’m not sure whether there is a known public-key cryptosystem that isn’t known to have a polynomial-time quantum attack.

There are plenty of triangle centres. One of the lesser-known triangle centres is Kimberling’s X(174), the Yff centre of congruence. It can be defined by considering lines known as isoscelisers, which are lines perpendicular to the angular bisectors of the triangle. If we’re careful, then they can intersect in such a way that three of the triangles formed (by an edge of the triangle and the isoscelisers of the two adjacent vertices) are congruent. This gives a degree of freedom:

The Yff central triangle is the case where the triangle formed by the three isoscelisers (red) is also congruent to the other three. When this triangle vanishes, we obtain the Yff centre of congruence. Apparently they’re named after their discoverer, Peter Yff, who was responsible for discovering several other triangle centres.

In particular, he rediscovered the second Morley centre. Morley’s theorem is quite a subtle result in Euclidean geometry, not least because the points concerned cannot be constructed by Euclidean methods. More precisely, they lie outside the field containing the vertices of the triangle and closed under the operation of taking geometric means. Anyway, the statement of the theorem is as follows:

Consider a triangle ABC. We form the point A’ by letting the angle trisector of ABC (closest to BC) meet the angle trisector of BCA (closest to BC). We similarly define B’ and C’. Then A’B’C’ is an equilateral triangle.

This is called the first Morley triangle. I seem to recall that if you take a cardioid inscribed within ABC, then its centre will lie on the perimeter of A’B’C’, and indeed the perimeter of A’B’C’ is the locus of possible centres. There’s a paper exploring this property and its relation to certain interesting cubics* in the plane of the triangle.

* You’re probably familiar with ‘interesting points’ (namely triangle centres), ‘interesting lines’ (such as the Euler line) and ‘interesting circles’ (the incircle, circumcircle, Euler-Apollonius lollipop etc.). In the same fashion, there are conics, cubics and higher-order algebraic curves passing through plenty of triangle centres.

Anyway, if we chose the other two angle bisectors and joined them, we would get a point A” opposite A’. Then, the triangle A”B”C” is also equilateral (it follows from the fact that, algebraically, it is defined in precisely the same way as the first Morley triangle), and called the second Morley triangle.

It can be shown that ABC, A’B’C’ and A”B”C” are in pairwise perspective (Desargues-style!), so we obtain three more points, P, Q and R, as perspectors. Taking these twelve points together with the nine lines of perspective and three of the original angle trisectors gives a self-dual projective configuration of 12 points and 12 lines discovered by Zacharias.

But then we can form its incidence graph! This is a bipartite symmetric cubic (3-regular) graph known as the Nauru graph. The etymology of this graph is derived from its drawing as a generalised Petersen graph, whose interior star polygon resembles the 12-pointed star on the flag of Nauru:

So, I guess it’s appropriate to explain the labels and coloured edges. We can think of this as the Cayley graph of the group S4 (with generators corresponding to transpositions (1 2), (1 3) and (1 4)), or as the map of admissible moves in a corresponding groupoid puzzle. I’ll describe the latter. We have four pedestals, each capable of accommodating precisely one Ferrero Rocher, of which we have one of each of three varieties. Then, on each move we can select a Ferrero Rocher and move it to the unoccupied pedestal. The graph of positions where edges correspond to legal moves is then the Nauru graph.

The Nauru graph has many other interesting properties such as symmetrical embeddings on a torus. David Eppstein investigated how these aspects are connected, and developed a theory of xyz graphs (basically cubic graphs that can be embedded as (possibly self-intersecting) orthogonal polyhedra). He has a series of articles on this topic, which, despite being on the same website, do not appear to share an index page. Hence, I’ll link to them here in chronological order:

1. Inverted permutohedron, exhibiting the first example of a xyz graph.
2. A projective plane in a 3d grid, which defines the concept of an xyz graph and explores a particular example, which is shown (by the easy classification of surfaces according to orientability and Euler characteristic) to be homeomorphic to the real projective plane.
3. Topology of xyz graphs, which expands on the previous ideas and realises all such compact surfaces (which can be formed by gluing finitely many handles and crosscaps to a sphere, as shown in The Symmetries of Things) as surfaces of immersions of xyz graphs.
4. 3-colouring and xyz graphs, which gives (rather beautiful) necessary and sufficient conditions for one to be able to convert a graph drawn on an abstract topological surface back into an immersion of an xyz graph, rather than the usual reverse process.
5. st-orientation and xyz graph recognition, which mentions the theory behind an exponential-time algorithm for recognising xyz graphs.
6. Ambiguously xyz, which exhibits an xyz graph that can be immersed in two distinct ways. It is proposed that this could be used as a method for reducing NP problems into the problem of determining whether a graph is an xyz graph, thereby strongly suggesting that there are no polynomial-time to perform xyz graph recognition.

Roughly at this point, he published the material in the form of a paper. However, later posts appeared, particularly involved with cubic symmetric xyz graphs (such as the Nauru graph itself). Indeed, we have:

7. Cubic symmetric xyz graphs, which is fairly self-explanatory.
8. More on cubic symmetric graphs.
9. The many faces of the Nauru graph, investigating embeddings on hyperbolic surfaces.
10. Not the Nauru graph.

As mentioned in a previous post, a pyritohedron is a (not necessarily regular) dodecahedron with pyritohedral symmetry. Up to scaling, any pyritohedron can be parametrised with the following coordinates:

• (±1, ±1, ±1);
• (±x, ±y, 0) and permutations thereof.

For the faces to be planar, we have a further constraint, Evaluating a basic 4-by-4 determinant gives the equation 2y = x + y², reducing the family of pyritohedra to have a single degree of freedom, h, where x = 1 − h² and y = 1 + h. Since there is only one degree of freedom, Bill Gosper realised that is particularly conducive to immortalising in a beautiful GIF animation, which he (for reasons unbeknown to me) entitled pyrominia.gif:

Let’s discuss each of these forms in further detail.

• We begin with the rhombic dodecahedron, a face- and edge-transitive polyhedron capable of tiling space in a face-centred cubic lattice arrangement. More precisely, it is the Voronoi cell of the lattice, that is to say the set of points closer to the origin than any other lattice point. Its projective dual is the cuboctahedron, one of the Archimedean solids.
• Next in the sequence is the well-known regular dodecahedron, one of the Platonic solids. Although the crystallographic restriction theorem precludes it from occurring in periodic crystals, there are pyritohedral approximations in iron pyrite (hence the name) and exact dodecahedral symmetry in certain quasicrystals.
• Not explicitly mentioned in pyrominia is one of the cells of the Weaire-Phelan structure. This is a more optimal soap bubble foam than the tessellation by truncated octahedra, the Voronoi cell of the body-centred cubic lattice (falsely conjectured by Lord Kelvin to be optimal).
• This is followed by the cubically degenerate pyritohedron, which marks the boundary between convex and concave pyritohedra.
• Next is the endo-dodecahedron. If you attempt to tessellate regular dodecahedra in the same arrangement in which one would usually tessellate rhombic dodecahedra, there is a small amount of empty space left over. The shapes of the holes are endo-dodecahedra, which are equilateral (all edges are of equal length).
• Eventually we reach the axes degenerate pyritohedron, beyond which the pyritohedra are self-intersecting.
• This is followed by another regular polyhedron, the great stellated dodecahedron. It is classified as a Kepler-Poinsot polyhedron rather than a Platonic solid, as it is self-intersecting and the Schläfli symbol (abbreviated form of a linear Coxeter-Dynkin diagram) has fractional values: {5/2, 3}.

Dihedral symmetry and pentiprisms

Julian Ziegler-Hunts discovered an irregular equilateral dodecahedron with dihedral symmetry, known as the pentagonal tympanohedron. It belongs to one of two infinite families of so-called pentiprisms (again a Gosperism), which resemble antiprisms but with pentagonal faces as opposed to triangles. The concave and convex families of pentiprisms are homeomorphic, as can be seen in this diagram (also by Gosper):

There is an exceptional hexagonal pentiprism, which is much flatter than the ordinary convex hexagonal pentiprism. Anyway, a few minutes ago Gosper created another animation, namely showing a deformation between a regular dodecahedron and the pentagonal tympanohedron:

Unfortunately, these dihedral forms are not as interesting as the pyritohedra. Nevertheless, half of the exceptional hexagonal pentiprism also occurs within the truncated triakis tetrahedron:

Do not be fooled into thinking that these faces are regular. If they were, we would have a Johnson solid. However, it is not possible to realise this in Euclidean space with regular faces, so it is known as a near-miss Johnson solid. Also be aware that the adjectives do not commute; a triakis truncated tetrahedron is a completely different solid (the Voronoi cell of the atomic structure of diamond), as mentioned in its Wikipedia article.

Incidentally, I seem to recall that I’m actually responsible for this confusion, as prior to a discussion between Tim Hutton and me, no-one had bothered to name this solid (despite it featuring in The Symmetries of Things). Following the standard nomenclature for systematically naming polyhedra, I entitled it the triakis truncated tetrahedron. Not long after, Tim Hutton created the Wikipedia article along with another for the corresponding tessellation.

This particular discussion spawned from Tim’s investigation of three-dimensional honeycombs on which to simulate reaction-diffusion systems and cellular automata. Tim was recently commissioned to use Ready to design a 40-foot bear sculpture with a reaction-diffusion texture!

Obviously, it inhabits a Baire space…

The 50-pence and 20-pence coins are regular curvilinear heptagons, where each edge is a circular arc centred on the opposite vertex.

One may ask why the coins have such an unusual shape. One possible answer is that it is impossible for a counterfeiter to forge with just a compass, straightedge and sheet of cupronickel. However, since compass-and-straightedge constructions are seldom used in practice, this is clearly not the reason.

This curvilinear heptagon has another property, which is easiest to demonstrate with its triangular analogue, the Reuleaux triangle. It is a curve of constant width, which means that all of its axonometric shadows are line segments of equal width. Equivalently, when rolled on a flat surface, the height of the coin remains constant.

The reason for employing a curve of constant width is that it can be more easily recognised by mechanical coin-detecting machines. The Reuleaux polygons are not the only curves of constant width, however, since we can easily design irregular curvilinear polygons with this property. Again, these are all piecewise circular.

The next question is whether there exist curves of constant width which are not piecewise circular. Intuitively, the answer is yes, since it seems plausible that a limiting process could be applied where the lengths of the circular arcs tend to zero. A more rigorous formulation is given by the following system of differential equations, where (as functions of t) are the endpoints of the line:

• a × k = b × k = 0 (both endpoints lie in the ij-plane);
• a’ · (a − b) = b’ · (b − a) = 0 (the endpoints move perpendicularly to the line segment, preserving its length);
• a’ × (a − b) · k ≥ 0 and b’ × (b − a) · k ≥ 0 (the endpoints move in the same direction);
• a(t + T) = b(t) and b(t + T) = a(t) (the curve is closed).

It transpires that there are algebraic curves other than the circle, which have constant width. One example is a degree-8 curve discovered by Stanley Rabinowitz.

Solids of constant width

The obvious generalisation of the Reuleaux triangle to three dimensions, the Reuleaux tetrahedron, does not have constant width. Nevertheless, Meissner demonstrated that it is possible to modify three of the edges of the tetrahedron to yield an actual surface of constant width, the Meissner tetrahedron.

Meissner tetrahedra can be obtained commercially from Maths Gear.

It is a well-known fact, attributed to Cantor, that the set of rationals is countably infinite or, equivalently, we can find a bijection between the rationals and integers. These are easy to construct, but typically quite ugly. If you want a closed-form bijection, you have to work harder, but it’s still possible.

My favourite enumeration of the (non-negative) rationals was discovered by Moshe Newman, and is a simple recurrence relation. More specifically, it is a very basic function f such that the sequence {0, f(0), f(f(0)), f(f(f(0))), …} contains each non-negative rational precisely once.

If you’re not amazed by this, you should be. It generates the sequence {0/1, 1/1, 1/2, 2/1, 1/3, 3/2, 2/3, 3/1, 1/4, 4/3, 3/5, 5/2, 2/5, 5/3, …}, which can be proved to hit every non-negative rational exactly once (indeed, if it repeated a rational, it would become cyclic). Also, note that the denominator of one term is equal to the numerator of its successor, yielding the following sequence of positive integers:

0, 1, 1, 2, 1, 3, 2, 3, 1, 4, 3, 5, 2, 5, 3, … (sequence A002847 in OEIS)

This sequence, Stern’s diatomic sequence, is highly intriguing. We define the nth term to be fusc(n), so fusc(0) = 0 and fusc(1) = fusc(2) = 1, for example. There are several equivalent ways to define the fusc function:

• The rational counter description gives the second-order recurrence relation fusc(n) = fusc(n−1) − fusc(n−2) + 2 fusc(n−1) floor(fusc(n−2)/fusc(n−1)).
• There’s also the David-Monk-style pair of recurrence relations, fusc(2n) = fusc(n) and fusc(2n+1) = fusc(n) + fusc(n+1).
• The previous definition can be seen to be equivalent to the definition of fusc(n) as the number of ways of writing n as a sum of powers of two, such that no power of two appears more than twice.
• fusc(n) is also the number of odd binomial coefficients of the form .

But yes, this is all pretty impressive. The sequence given by Newnham’s rational counter is a breadth-first traversal of the Calkin-Wilf tree, as shown below in this picture by David Eppstein:

Each node has children and . It is a routine exercise (which, I believe, has appeared on the British Mathematical Olympiad) to show that each positive rational appears precisely once in this binary tree.

Breaking news: A £500 prize for the most elegant solution in the British Mathematical Olympiad has been founded in the memory of Christopher Bradley, whose contributions to the United Kingdom Mathematics Trust were both plentiful and invaluable. Amongst his portfolio is the bestselling Plane Euclidean Geometry (coauthored with Anthony Gardiner), which explores the interactions of algebraic curves of low degree in two dimensions from a synthetic perspective.

The advantage of this new prize is that it discourages ridiculously long case-bashes, thus making the BMO easier for us to mark. Some case-bashes are long but morally simple, such as the proof of the four-colour theorem, and it is difficult to assess whether such proofs are elegant. Nevertheless, in most cases it is easy to distinguish between an elegant solution and an inelegant one. For instance, consider the following problem:

What is the maximum number of subsets of {1, 2, 3, …, n} such that no subset is a subset of a different subset?

If we choose subsets of the same cardinality, then it’s obvious that these would satisfy the criterion. For example, with {1, 2, 3, 4} and choosing the size-2 subsets, we obtain the following six sets:

• {1, 2}
• {3, 4}
• {1, 3}
• {2, 4}
• {1, 4}
• {2, 3}

This strategy is maximised when the cardinalities of the subsets are as close to ½n as possible. It is difficult to imagine a more optimal solution, and it is a theorem (Sperner’s theorem) that this is actually the best we can manage.

Anyway, a trivial rephrasing of the problem is:

What is the maximum length of an antichain in the lattice of subsets of {1, 2, …, n}, ordered by inclusion?

By Dilworth’s theorem (a corollary of max-flow min-cut), this is equivalent to:

What is the minimum number of chains into which we can partition the lattice of subsets of {1, 2, …, n} ordered by inclusion?

We can think of the subsets of {1, 2, …, n} as being vertices of a hypercube. All of the automorphisms of the hypercube fixing the vertex corresponding to the empty set are symmetries of Sperner’s theorem.

It would be nice to have a generalisation of this theorem which has all automorphisms of the hypercube as symmetries (i.e. the empty set is not given privileged status). Such a generalisation was very recently discovered by Hunter Spink in the process of proving an open problem about the maximum number of strict maxima of quadratic functions of n Boolean variables. The short but exciting paper can be found here.

So, yes, Hunter Spink is rather awesome. We were discussing the completely unrelated topic of the existence of a ‘romantic’ clearing between a Salix and a Sorbus just south of the bridge of King’s College, Cambridge. It is only just possible to punt into the clearing, perform a U-turn, and exit.

The clearing at 52.203650° N, 0.113854° E.

As I was describing this, Richard Freeland mentioned the well-known problem of finding the clearing with minimum area corresponding to the constraint that one can rotate a punt (considered to be a line segment) 360° within it. A reasonably good solution is the deltoid:

Surprisingly, it transpires that there is no minimum area attainable. For every positive ε, we can find a simply-connected set of area < ε in which a punt can be rotated. However, the infimum of 0 cannot be obtained, i.e. there is no set of zero Lebesgue measure in which we can rotate a punt (c.f. this proof by Terence Tao). There are, however, measure-zero fractal sets obeying the strictly weaker property of containing a unit line segment in every orientation, so-called Besicovitch sets.

Generalisations to have been considered, but this problem was found to be very difficult. As a compromise, people contemplated the analogy over finite fields: fix n > 2 and let p vary. Then, we can find a non-zero lower bound for the density of a Besicovitch set (containing a line in every direction) in the vector space , depending only on n and not p.

Dvir found a beautiful proof (which would certainly win Bradley’s elegance prize!), again mentioned in an article by Terry Tao.

Here are some primarily mathematical double-entendres conceived by members of the Trinity Mathematicians’ Alcoholic Society. Some of them are biological or particle-physical, but never mind. Also, some names are censored for legal reasons.

Disclaimer: I accept no responsibility for any offence caused by these; if you’re offended, comment and I shall endeavour to respond to the best of my ability.

• I’m like the Riemann zeta function; I have a massive pole — Emperor of TMAS (me)
• You put a whole new angle on — Empress of TMAS
• I’m so smooth, I’m infinitely differentiable — Vice-President of TMAS
• I’m like the blancmange function; I’m tasty and not well-behaved — Emperor of TMAS (me)
• You’re a photon, because you make my light shine — First Gentleman of TMAS
• If I were an enzyme, I’d be helicase so I could unzip your genes — Humphrey Galbraith, nephew of Lord Strathclyde
• You’re the integral of — Joe Tomkinson
• I wish you were my maths example sheet, because then I’d turn up to my supervision and explain why I didn’t do you properly — Vice-President of TMAS
• If I were endoplasmic reticulum, would you like me rough or smooth? — Sara Devereux
• I wish you were my maths example sheet, because I’d do you even if I didn’t understand you. — First Gentleman of TMAS
• I wish you were an integral, because then I could substitute and do you anyway — Humphrey
• My girlfriend is like the integral of ; I can’t do her without cheating — Vice-President of TMAS
• I wish you were my multiplicative inverse, because together we’d be one — First Gentleman of TMAS
• I wish I were your derivative, because then I could lie tangent to your curves — a fellow RMM gold medallist
• If I were a Schwarz cell, I’d be on your axon for some fast-action potential — Anonymous
• My love for you is unbounded and monotone increasing — Empress of TMAS
• She’s like an asymptote; I get closer and closer but never reach her — Communal effort
• If I were , you would be ; I’d be contained in you — Ryan Wilson
• Our intersection is very pleasurable, let’s try our union…? — Joe Tomkinson
• Particle physics really gives me a hadron — First Gentleman of TMAS
• If you were , I’d be , because then we’d be osculating — the same fellow RMM gold medallist
• Our love is like the naturals and the ocean floor; it’s deep and infinite — First Gentleman of TMAS
• I’m like a rigorously proved theorem; I can last forever — Emperor of TMAS (me)
• Are you an electron, because then you’d be lepton? — Anonymous
• You are my only element; without you I’d be empty — First Gentleman of TMAS
• You’re like a sporadic group, beautiful and mysterious — Emperor of TMAS (me)

You have probably encountered the 15-puzzle, where all but one of the squares of a 4 × 4 grid are occupied by counters. The only acceptable moves are to move a counter into an adjacent unoccupied square.

Sam Loyd challenged people to swap a pair of adjacent counters. It is relatively easy to show that this is impossible, as changing the parity of the permutation of the sixteen objects (fifteen counters and one empty space) also changes the parity of the position of the empty space.

Unlike the Rubik’s cube, the set of positions in this puzzle do not form a group. Instead, they form a groupoid, since two operations can only be composed if the final position of the empty space in the first operation is equal to the initial position of the empty space in the second operation. Groupoids have the same axioms as groups, except for totality; it is not always possible to compose two arbitrary elements.

Conway, Elkies and Martin created a similar, albeit more interesting, puzzle. Place a counter on each of 12 of the 13 points of the projective plane of order 3. The plane has 13 lines of four points, and the following operation is allowed:

• Select a counter, move it into the empty space, and swap the two remaining counters on that line.

The groupoid generated is known as M13, since it has connections with the Mathieu groups. In particular, the subgroup of positions fixing the empty space is isomorphic to M12. M12 itself has been realised as the group of positions accessible with a mechanical puzzle. In fact, I know of at least three such descriptions, which are completely different:

• Twelve ball-bearings touch a central sphere in an icosahedral arrangement. M12 is generated by pairs of clockwise and anticlockwise twists (where we choose an equator orthogonal to a diameter joining opposite spheres, and rotate one of the two hemispheres).

• The Number Planet mechanical puzzle by Oskar van Deventer and Jim Stasheff:

• The Topsy-Turvy puzzle, also by Oskar van Deventer:

[youtube=http://www.youtube.com/watch?v=H8ZcYvU0sLY]

There are electronic implementations of M12, M24 and Co0 as puzzles, designed by Igor Kriz whom you may recognise from his work in Euclidean Ramsey theory.