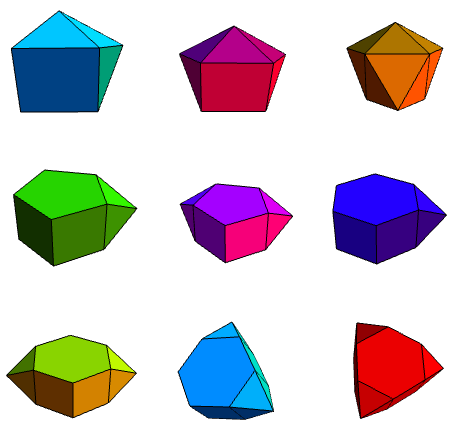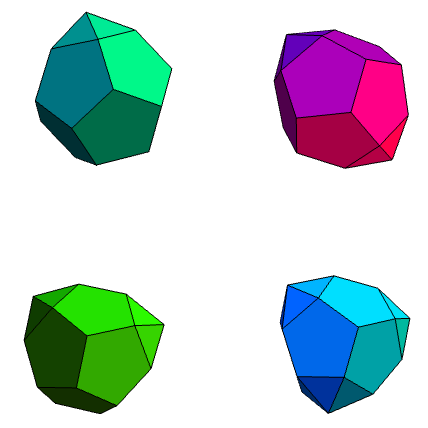Complex Projective 4-Space

Assorted news

Posted on June 22, 2013 by apgoucher

Firstly, the bounded gaps between primes project has made a considerable amount of progress since the value of H = 285278. The latest result has the following parameters:

v08ltu’s bounds, leading to a value of H = 12012.

Tables of admissible k-tuples had already been precomputed, so Terence Tao was able to consult them to find that this gives an upper bound of H = 12012. This is also dangerously close to Ben Green’s estimate of 10000 as being the smallest value of H provable using these sieve methods. Again, updated information can be found on the polymath page.

In other news, a book has been published refounding mathematics upon a recent hybridisation of homotopy theory and type theory. It is intended to be more machine-checkable than ZFC set theory, which has been used as the foundation of mathematics since Nicolas Bourbaki*. Also, category theory cannot be founded in ZFC set theory, since many of the categories are proper classes (too large to be sets).

* Nicolas Bourbaki was a set of mathematicians, rather than an individual mathematician.

Posted in Uncategorized | Leave a comment

Iterated Aut revisited

Posted on June 19, 2013 by apgoucher

In an earlier post, I briefly mentioned the idea of repeatedly iterating the Aut operator (a function which takes an abstract group as its input and outputs the automorphism group) and observing the behaviour. There have been papers on the transfinite version of this problem, and a few of the theorems are applicable here. Other results can easily be proved from first principles.

If Aut(G) is Abelian, then G is cyclic.
If Aut(G) is cyclic, then |G| is either 1, 2, 4, a power of an odd prime, or twice a power of an odd prime.
If G is a non-Abelian simple group, then Aut(G) = Aut(Aut(G)).
If G is centreless, then its automorphism group is also centreless. Moreover, the automorphism tower stabilises in a finite time, resulting in a complete group.

The tree of ancestors of the trivial group is straightforward to compute. It consists entirely of cyclic groups, the orders of which form sequence A117729 in the OEIS. I’ve sketched the first few terms of this tree:

Since there are so many groups, I decided to concentrate on observing the behaviour of cyclic groups under iteration of the Aut operator. The automorphism group of the cyclic group of order n is an Abelian group, namely the multiplicative group of totients modulo n. We’ve already covered orders up to and including 7 in the above tree, so let’s see what happens to the cyclic group C8. We first get the Klein 4-group, and then the symmetric group S3:

In this case, S3 arises as the general linear group over the vector space (F2)². This applies to any direct sum of Cp cyclic groups, such as (F2)³. We get the general linear group GL(3,2), which happens to be isomorphic to PSL(2,7). Its automorphism group is PGL(2,7), which is a complete group (centreless group with no outer automorphisms), and therefore maps to itself.

So far, all of the ‘terminal groups’ have been complete groups. It turns out that our next cyclic group, C15, will result in a group which is equal to its own automorphism group despite not being centreless. In essence, the existence of a non-trivial centre cancels out the outer automorphism.

In the existing literature, people treat the Aut operator as more than a function on the set of finite groups, and generalise this to a transfinite process. Indeed, they do not consider D8 to have ‘stabilised’, since it is not a complete group, but rather declare that it terminates in ω + 1 steps, with the ωth iterate being the cyclic group C2. It has been proved that these transfinite automorphism towers always terminate. Here, however, we are only interested in isomorphism classes of groups, and finite iterates of the Aut operator, so for our purposes D8 is a terminal group (a group isomorphic to its automorphism group).

The next cyclic group unaccounted for, C21, also stabilises as a dihedral group, namely D12. It is more helpful to visualise this as the direct product of S3 and C2. Again, this is not a complete group, since it is not centreless.

Along similar lines to how the general linear group can arise, we also obtain general affine groups. C67, for example, culminates in the direct product of S3 with the general affine group of (F2)², which happens to be S4. This is a direct product of two characteristic groups, so its automorphism group is the product of their automorphism groups. As S3 and S4 are themselves complete, the chain terminates here.

Central and wreath products

As we progress further, computing automorphism groups becomes very difficult. Take the cyclic group C32, for example. Its automorphism group is C2 × C8, and the automorphism group of that can, with some little work, be shown to be C2 × D8. What about the automorphism group of that? It is not too difficult to show that it is the group obtained by placing a lightbulb on each of the vertices of a rectangle, and considering the group generated by Euclidean transformations of the rectangle together with toggling an even number of lightbulbs.

That group has order 32, and is generated by the twelve elements of order 4. Draw an edge between two of these elements if they do not commute with each other; the resulting graph is a pair of disjoint octahedra:

So, we have something vaguely similar to a direct product. It transpires that it’s actually the central product of Q8 with itself, obtained from the direct product by quotienting by the common centre (−1, −1). We denote this by Q8 * Q8.

It can be shown that the automorphisms of Q8 * Q8 are products of automorphisms of the individual Q8s, and an automorphism exchanging the two copies of Q8. As the automorphism group of Q8 is the symmetric group S4 (the rotational symmetries of an octahedron), the automorphism group of Q8 * Q8 is the wreath product S4 wr C2. We can think of this as the rigid motions of two identical octahedra; we can rotate them individually or permute them.

I suppose, at this point, I should explain what a wreath product is. I find that it’s rather intuitive to understand, and best explained by considering a few examples. Firstly, if we have a wreath product A wr B, it is necessary for B to act on a set X. We then define A wr B as acting on the set A^X (the set of ways to label the elements of X with elements of A), generated by the action of B permuting the elements of X, and the action of A^X on A^X by pointwise multiplication.

For example, C2 wr Z (where Z is the infinite cyclic group, acting on the integers by translation) is the lamplighter group, generated by translations of an infinite line of lightbulbs and by toggling any subset of the lamps.

For all n other than 2, 3 and 6, we have Aut(An) = Aut(Sn) = Sn. For n = 6, the automorphism group of A6 and S6 is the projective semilinear group PΓL(2, 9), which is twice as large (with order 1440, instead of 720). This is a result of the exceptional outer automorphism of S6.

As a challenge, try tracking the behaviour of the prime cyclic group C227. (Hint: you’ll need to know lots of four-dimensional geometry!) If you give up, it’s included on this beautiful colour-coded poster, along with many other groups.

Infinite growth?

We conjecture that infinite growth is possible, and that the sequence C61 → C60 → C2 × C2 × C4 → D4 → F4/Z × C2 → (S4 wr C2) × C2 → (S4 wr C2) × C2 × C2 → (S4 wr C2) × S4 × C2 × C2 → (S4 wr C2) × S4 × S4 × C2 × C2 × C2 × C2 → … is such an example. It appears to result in arbitrarily many copies of C2 being produced, thereby expanding infinitely. We haven’t ruled out the possibility that the other groups produced in the process could interfere with this and prevent further growth, and it seems extremely difficult to prove that there exists a group capable of infinite growth.

If infinite growth is possible, it would be unsurprising if it is undecidable whether a generic finite group terminates or grows indefinitely. Indeed, it may even be possible that there exists an algorithmic procedure for converting a Turing machine into a group, which terminates under iteration of Aut if and only if the Turing machine halts. If this is the case, it is probably the most difficult Turing-complete programming language in existence.

Posted in Uncategorized | 9 Comments

Cipher 32: Untitled

Posted on June 18, 2013 by apgoucher

This was not the cipher I originally intended to make, but rather a compromise due to time constraints. Also, my complete lack of imagination is manifested in the fact that this cipher lacks a title. The only elegant property is that the number of blocks in the ciphertext is precisely the index of the cipher.

Enjoy.

Posted in Ciphers | Leave a comment

How to score 1729 in the IA Tripos

Posted on June 16, 2013 by apgoucher

Part IA of the Mathematical Tripos is marked in a rather interesting way. A naïve computation of the maximum score is 1120, although it is (in principle) possible to achieve absolutely any score (it need not even be a real number!). Firstly, let’s have a look at the scoring system:

A long question carries 20 raw marks. A score of 15 or more results in an alpha being awarded; a score of between 10 and 14 results in a beta being awarded. A candidate can be scored on a maximum of twenty long questions.
A short question carries 10 raw marks. A score of 8 or more results in a beta being awarded.

The alphas and betas are subsequently converted into marks according to the following scheme (quoted from the schedules of the Mathematical Tripos):

The −120 is generally referred to as an alpha tax, and cannot hurt you if you score eight or more alphas. However, if you score seven or fewer alphas and still get a first, you are actually penalised by the alpha tax. Suppose Miranda scored the following marks in 2012 (when the threshold for a first was 670):

10/10 on all sixteen short questions;
20/20 on five long questions;
14/20 on fifteen long questions.

Then, she would have a raw mark m = 470, together with 5 alphas and 31 betas. Now, each of the following two implications are perfectly valid:

If Miranda achieves a 2.1 (any lower grade is impossible), then her total merit mark would be M = 470 + 15 × 5 + 5 × 31 = 700, which is sufficient for a first. Hence, Miranda achieves a first class degree.
If Miranda achieves a first class degree, then the alpha tax would apply, and her total merit mark would be M = 470 + 30 × 5 + 5 × 31 – 120 = 655, which is insufficient for a first. Hence, Miranda achieves a 2.1.

In other words, we have a paradoxical inconsistency! Consequently, Miranda could then apply something called the Principle of Explosion, exploiting the fact that any valid proof is taken to be perfectly correct in the Tripos. Specifically, she makes the following sequence of deductions:

By the Law of Excluded Middle, either the alpha tax applies or it does not. Let α be the proposition that the alpha tax applies. We have already established the implications that α ⇒ ¬α, and ¬α ⇒ α. Hence, both ¬α and α are true statements. Let φ be the proposition that Miranda scores 1729 on the IA Tripos. Since the logical disjunction of a true statement and an arbitrary statement is true, we have φ ∨ α. However, since ¬α is true, α is false and therefore φ must be true. Consequently, Miranda scores 1729 on Part IA of the Mathematical Tripos, thereby beating anyone who scored full marks on all questions.

Essentially, the Principle of Explosion states that if a proposition and its negation are both true, then all propositions are true. This is why it is important that axioms of set theory are consistent, as a single inconsistency would destroy mathematics.

Posted in Uncategorized | 5 Comments

Quasifractals

Posted on June 15, 2013 by apgoucher

One of the more familiar examples of fractal curves is the Koch snowflake. It is a closed curve of infinite length and Hausdorff dimension log(4)/log(3), homeomorphic to the unit circle. It bounds a region which, when combined in two different sizes, can tile the plane (as noted by Benoit Mandelbrot):

The Koch snowflake can be constructed from three copies of the von Koch curve. This is a self-similar fractal curve, composed of four copies of itself, each scaled by $\sigma = \frac{1}{3}$ . Varying the value of σ between ¼ and ½ yields a family of fractal curves, with Hausdorff dimension ranging from 1 (a straight line) to 2 (a spacefilling curve):

In each of the curves, the same value of σ is used for all iterations. If, instead, we vary the value of σ, then the Hausdorff dimension is a function of the limiting value of σ (assuming the limit exists). In the following curve, σ successively takes on the values {1/4 + 1/5, 1/4 + 1/6, … , 1/4 + 1/n, …}, so the limiting value of σ is ¼, and the Hausdorff dimension is 1. Hence, this is not technically a fractal. However, an easy computation will verify that the length (product, over all iterations, of 4σ) is infinite.

$quasifractal$

In other words, we have a non-fractal curve that nevertheless exhibits many of the same properties as fractal curves (infinite length, approximate self-similarity, etc.). On the other hand, if the values of σ converge to ¼ sufficiently quickly, then we obtain a curve of finite length.

Posted in Uncategorized | 2 Comments

Plateau

Posted on June 13, 2013 by apgoucher

Given two identical circles lying in parallel planes with a common axis of symmetry, what is the minimal surface that connects them? Initially, one might suppose that it is a cylinder (blue in the diagram below).

However, we can quickly establish that a cylinder is not favourable. For a minimal surface, optimal solutions have zero mean curvature, whereas the cylinder has nonzero mean curvature. The correct solution is a catenoid (green), which is the revolute of the curve $cx = \cosh{cz}$ about the z-axis; this can be demonstrated by the calculus of variations.

Another minimal surface is the helicoid, obtained by taking the surface swept out by a horizontal line undergoing a continuous screwing about a vertical axis. Indeed, there is actually a continuous distance-preserving map from the helicoid to the catenoid, describable as a complex rotation:

Obviously, a boring example of a minimal surface is the plane. Indeed, when the two circles are sufficiently separated, the catenoid is no longer optimal and a pair of disjoint discs is instead minimal.

Suppose that the circles are replaced with impenetrable discs, and we inject a prescribed volume of air into the catenoid. The requirement is no longer that the surface have zero mean curvature everywhere, but rather constant mean curvature. In this generalisation of the problem, the cylinder is optimal for a particular value of the volume.

In the simplest case, where we have a fixed volume and no constraints on the boundary, a sphere is optimal; this is why individual bubbles form spheres. It took until 2002 for this result to be extended to two volumes of air; the optimal solution is a set of three spherical films, meeting at a common circle at angles of 2π/3.

Plateau proved that all such edges between three films must be at angles of 2π/3 (c.f. this post), and vertices where four such boundaries meet must locally resemble regular tetrahedra. Together with the requirement that mean curvature must be constant on any film, we obtain Plateau’s laws.

Lord Kelvin wondered what the optimal arrangement of soap bubbles of unit volume is, so as to minimise the total surface area. He conjectured that the regular honeycomb of truncated octahedra was optimal, and for a while the Kelvin conjecture was believed to be true.

Actually, Kelvin slightly curved the faces to conform to Plateau’s laws. It transpires that there is a better polyhedral tiling giving a more optimal arrangement of soap bubbles, discovered by the Irish mathematicians Weaire and Phelan in 1994. John Conway refers to these as Scottish and Irish bubbles, and proposes a third system of Welsh bubbles. They haven’t caught on, however; the Kelvin structure occurs as the Voronoi partition of many crystal structures, and the Weaire-Phelan structure was used in the architecture of the Beijing Natural Aquatics Centre for the 2008 Olympic Games:

Posted in Uncategorized | Leave a comment

Cipher 31: Polyphasic

Posted on June 11, 2013 by apgoucher

Firstly, I’ve been assigned the task of advertising the final episode of Magpie and Stump, which takes place at 21:30 in the Winstanley Lecture Theatre of Trinity College this Thursday (13th June 2013). It will be absolutely epic, and even if you live in another country, it’s definitely worth visiting for the day; you won’t be disappointed.

After two weeks of cryptographic inactivity, I am pleased to announce that the second season of cp4space ciphers is now commencing. For the (thirty-)first cipher, I have borrowed inspiration from a particular Russian cipher.

27446161737957865771637155886819508150245288536777083311
61635461109767135088525857581361414871617379578646882123
57795047840718611888530441032364574125613789708089187361
97285197524561600358116337081161774609632938506948791466
57525104778201684228519752456161897974641083510457581361
36976600137838815723708089187031518251311988508829374168
53085682408727910789708089187361972851975245616767876601
79997191563421215588452109100361594761230787073117865187
52842161838318615507205154847160659946065088550657581361
61874586678603415398586777883358575251311988681950815024
52885367770833116163546164076160074453675749517381342950

As before, there is a secret area that can only be accessed with a password provided in the encoded text. The link to this area can be found in the usual place.

Posted in Ciphers | Leave a comment

Down to 285278

Posted on June 9, 2013 by apgoucher

After Zhang established the result that there are infinitely many pairs of primes separated by at most 70000000, there has been a massively collaborative effort to reduce this bound. The efforts are concentrated on developing methods to strengthen each of three variables in the original paper:

The pair of real parameters (ω, δ), which were equal in the original paper, but later separated so that they can be optimised independently. Current efforts are to increase the value of ω in the hope of obtaining a smaller value of:
The integer k0: This is a positive integer such that for each admissible set S of k0 integers, there are infinitely many translates S + n containing at least two primes. An admissible set is one where, for each prime p, there exists a residue class $a + p\mathbb{Z}$ disjoint from S. At the moment, there is an established upper bound of 26024 and a conditional result by Terry Tao et al claiming that $k_0 \leq 10719$ . Reducing the value of k0 leads to a smaller value of:
The integer H, which is the diameter of the smallest admissible set of size k0. For each k0, it is possible to find upper bounds (using sieves to construct admissible sets) and lower bounds (obviously, k0 is a trivial lower bound, but certain inequalities such as Montgomery—Vaughan provide much tighter bounds). More details are here.

For the last few hours, the progress has rather resembled a game of tennis between Andrew Sutherland and xfxie, with the world record for H being repeatedly tossed between them. At the moment, Sutherland is winning, having reduced H down to 285278. You can get a slice of the action by viewing this comments thread, and perhaps chiming in with a smaller admissible set*.

As you can see, Sutherland has introduced a new optimisation together with a rather colourful piece of new terminology to describe it! This technique can sometimes lead to incremental (or should that be excremental?) reductions in the upper bound for H.

* Entries are to be given as a list with the filename admissXble_YYYYY_ZZZZZZ.txt, where X is a vowel used to specify the author (i for xfxie and a for Sutherland; you can choose any other vowel in your surname), YYYYY is the size of the set (preferably one of the established or conditionally proved values of k0), and ZZZZZZ is the diameter (an upper bound for H, assuming your value of k0 is correct). Examples are admissible_26024_286216.txt and admissable_10719_108514.txt.

We’re still waiting for confirmation that the value 10719 is valid; if so, the upper bound on H will drop from 285278 to 108514 — a significant improvement, but still considerably far from the desired target of 2. Here’s the timeline at the moment:

For continually-updated data, consult the polymath page.

Posted in Uncategorized | 5 Comments

Johnson solids

Posted on June 8, 2013 by apgoucher

In 1966, Norman Johnson completely classified all of the strictly convex polyhedra with regular polygonal faces. It is a remarkable fact, but not too difficult to prove, that there are precisely two infinite families (the prisms and antiprisms), together with a large but finite number (108) of exceptional objects.

Firstly, by strictly convex, we mean that the shape is convex, and that no three vertices are collinear. Hence, we rule out possibilities such as this 24-faced cube:

To prove that there are no infinite families other than the prisms and antiprisms, we will first establish a lemma:

Lemma: If a strictly convex solid with regular faces has a face with 20 or more edges, then the solid is either a prism or antiprism.

Proof: We consider the possible vertex figures around each of the vertices of the n-gon (where 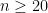$n \geq 20$ ). By angle constraints, we can narrow down the vertex figures to (n.3.3.3), (n.4.4) and (n.3.6). These are shown below:

We can eliminate the n.3.6 configuration, by considering the other vertex where the triangle and hexagon meet. By the symmetry of the hexagon-triangle configuration, the only way to complete this is to add another n-gon; this would intersect the first n-gon, thereby rendering it invalid.

The n.4.4 and n.3.3.3 vertex configurations therefore automatically ‘induct’ to all vertices of the n-gon. This results in partial prisms and antiprisms, which (due to strict convexity) can only be completed by capping with another n-gon. This completes the proof of the lemma.

Theorem: There are only finitely many strictly convex solids with regular faces, other than the infinite families of prisms and antiprisms.

Proof: As there are only finitely many admissible faces (since 20-gons and higher are forbidden by the lemma), there are only finitely many possible vertex figures. Each one has a positive vertex angle defect (a discrete analogue to curvature), and the sum of the vertex angle defects must be 4π (known as Descartes’ theorem). This provides an upper bound for the number of vertices, which then upper-bounds the number of abstract polyhedra, and therefore the number of polyhedra (up to possible flexing). However, the rigidity theorem tells us that convex polyhedra cannot flex, completing the proof of the theorem.

The classification of finite strictly convex polyhedra with regular faces

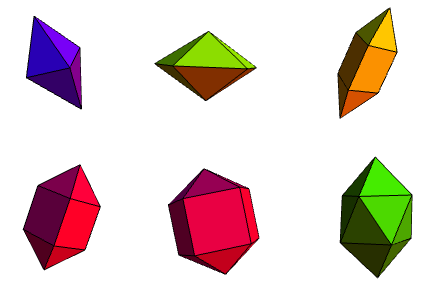
Now that we have two infinite families, it would be a good idea to look for other solids. The simplest are the remaining three Platonic solids (the cube and octahedron are a prism and antiprism, respectively).

As we know, we can also get another 13 Archimedean solids by modifying them with certain operations. It turns out that there are precisely 92 non-uniform strictly convex polyhedra with regular faces, known as Johnson solids. By analogy with the tetrahedron, we can also have a square pyramid (J1) and pentagonal pyramid (J2):

These can also be thought of as extremal mutilations of the octahedron and icosahedron, respectively. Similar processes can be applied to Archimedean solids, resulting in three cupolae and the pentagonal rotunda:

These are J3, J4, J5 and J6, respectively, in Johnson’s classification. Note that when we constructed the pentagonal pyramid, we did so by slicing an icosahedron. The remaining piece is a gyroelongated pentagonal pyramid (J11), which can itself be regarded as a union of a pentagonal pyramid and pentagonal prism. This opens up a whole new world of possibilities of joining pyramids to prisms and antiprisms (giving J7 to J11, inclusive):

The octahedron is essentially two square pyramids, fused at their bases. The icosahedron is two pentagonal pyramids, connected by a pentagonal antiprism. We can repeat these types of constructions with other pyramids, yielding another six Johnson solids (J12 through to J17):

J7 through to J11 were constructed by elongating/gyroelongating pyramids. This can also be applied to the cupolae and pentagonal rotunda, yielding J12 to J25, inclusive.

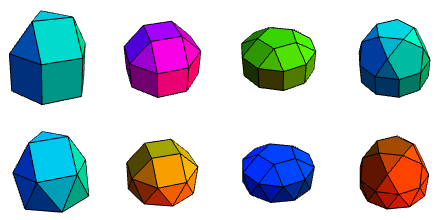
In each case, the elongated form is displayed directly above the gyroelongated form. I’m not sure that I can easily motivate the next solid in the classification, which is a combination of two triangular prisms, meeting at a square face. It does have the very imaginative name, gyrobifastigium (J26), considering how simple and banal it is.

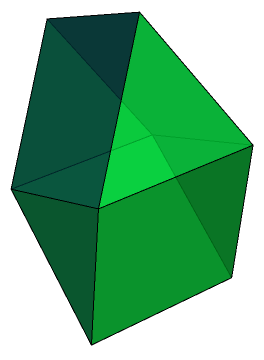
The most interesting thing about the gyrobifastigium is its etymology. The prefix bi- is obviously due to the fact that there are two triangular prisms. The gyro- describes how one is rotated with respect to the other, as opposed to having bilateral symmetry in the plane where they meet. But fastigium? Apparently, it is the Latin word for a summit, peak, or apexed roof.

Let’s return to the systematic construction of more Johnson polyhedra. J12 and J13 were built out of two pyramids, base-to-base. Replacing ‘pyramid’ with ‘cupola’ or ‘rotunda’ gives another eight Johnson solids (J27 to J34):

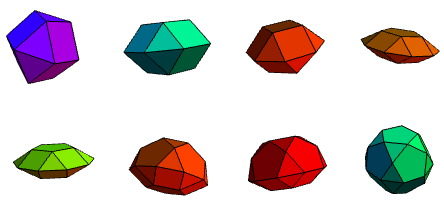
These, as with the other Johnson solids, have very systematic names such as triangular orthobicupola and pentagonal gyrocuploarotunda. Recall that J14 to J17 simply involved introducing interstitial prisms and antiprisms to the bipyramids; this trick also works here to give some more solids. Firstly, for the triangular bicupolae, we obtain elongated forms:

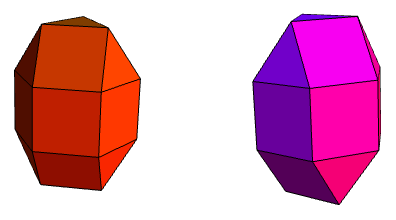
If we repeat for the square cupola, we only get one new form. The elongated square orthobicupola is just a rhombicuboctahedron (an Archimedean solid). By comparison, the elongated square gyrobicupola (J37) is an evil impostor, which has the same circumradius, inradius, midradius and volume as the rhombicuboctahedron, as well as the same quantities of each of the different faces, and even the same vertex figures on every vertex. More remarkably, it can even be shown that they have the same inertia tensor.

To an untrained observer, they look very similar, and you may even be able to convince multiple people for several hours that they are, in fact, looking at a rhombicuboctahedron. Sooner or later, however, people will start to suspect that it is merely a very convincing lookalike, noticing slight problems such as lack of vertex-transitivity, and the fact that it only has one equator of eight squares, rather than three.

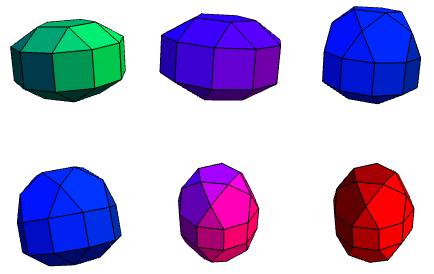
Shown above are six elongated pentagonal forms. There are also five gyroelongated forms, shown below:

New polyhedra from old

We’re now just over halfway through the classification of Johnson solids. The next big idea is to erect pyramids on the faces of existing solids to produce new forms. Again, we’ll start with prisms, yielding another nine solids (J49 to J57):

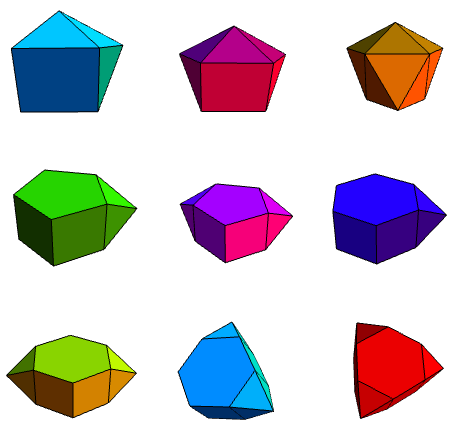
Johnson refers to pyramid erection as augmentation. Consequently, the top three solids are the augmented, biaugmented and triaugmented triangular prisms (J49, J50 and J51, respectively). Similarly, we get augmented and biaugmented pentagonal prisms (J52 and J53), and an augmented hexagonal prism (J54). However, both J56 and J57 could be called biagumented hexagonal prisms, so we need a way to distinguish between them. Johnson decided to borrow terminology from organic chemistry, used to describe the relative positions of functional groups on a benzene ring:

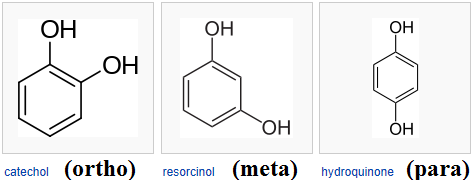
This terminology also comes in handy for dodecahedra. We have augmented, parabiaugmented, metabiaugmented and triaugmented dodecahedra (J58 to J61):

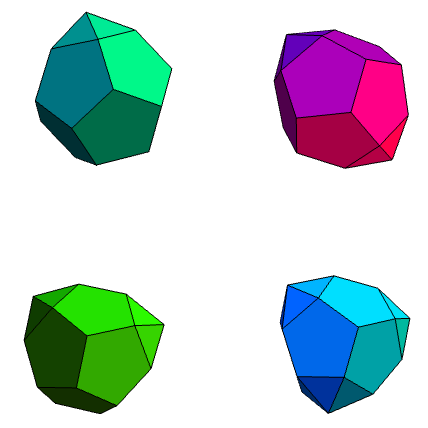
The reverse operation to augmentation is diminshing. The diminished and parabidiminshed icosahedra are the gyroelongated pentagonal pyramid and pentagonal antiprism, respectively. However, the metabidiminished icosahedron (J62) and tridiminished icosahedron (J63) are genuinely new forms. Adjacent to the three pentagonal faces of J63 is a triangular face, which can (only just!) accept an erected tetrahedron, giving an augmented tridiminshed icosahedron (J64). These three solids are shown below:

The next few solids are obtained by augmenting truncated regular solids not with pyramids, but with cupolae.

Again, their dodecahedral counterparts require prefixes to distinguish between the two biaugmented truncated dodecahedra.

The next set of Johnson solids comes from modifying the rhombicosidodecahedron. In the same way that we can obtain the elongated square gyrobicupola (J37) by rotating a cupola of a rhombicuboctahedron, we can also gyrate the rhombicosidodecahedron. Additionally, it is possible to diminish it (by removing a cupola completely), or even perform different operations to different cupolae. Twelve new solids (J72 to J83) arise in this manner:

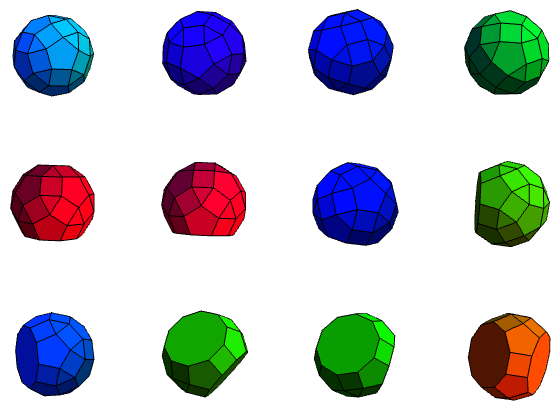
The top four are quite difficult to differentiate from each other. A systematic way is to look for pentagons and triangles sharing faces (there will be adjacent squares, which are easier to spot, nearby), to highlight the triangle, and to highlight pentagons which five highlighted triangles ‘point to’. Then, the highlighted pentagons correspond to gyrated cupolae.

Finally, there are nine additional Johnson solids (increasing the total to 92), which are ‘primitive’ and cannot be derived from modifying existing solids.

The first of these is called a snub disphenoid, which is a rather stupid name since snubbing a disphenoid would produce a polyhedron abstractly equivalent to a snub tetrahedron, i.e. an (irregular) icosahedron. Again, we have some interesting names, such as hebesphenomegacorona (J89) and disphenocingulum (J90).

And now you’ve seen them all.

Posted in Uncategorized | 11 Comments

The Not-Very-Random-At-All Graph

Posted on June 6, 2013 by ggendler

This is a guest post by Gabriel Gendler. As such, any views expressed in this post do not reflect the views of Complex Projective 4-Space or of Adam P. Goucher.

In a recent post Adam P. Goucher recommended that readers adopt the Petersen graph as their favourite graph, if they had not chosen one already. This post is designed to promote an alternative favourite graph – the Rado graph.

Definition

We start with the following, seemingly tame, definition. Define the countably infinite graph $R$ with vertex set $V(R) = v_0, v_1, v_2 \ldots$ ; the edge set is $E(R)$ , and for $i<j, (v_i, v_j) \in E(R)$ if and only if in the binary expansion of $j$ , the digit $i$ from the right is 1. So, for example, $v_0 \sim v_k$ for odd $k$ and $v_1 \sim v_k$ for $k \equiv 2$ or $3 \pmod 4$ .

The extension property

First, we observe a useful but not immediately interesting property: for any finite disjoint sets of vertices $V, W \in V(R)$ , there exists a vertex $x \notin V \bigcup W$ such that $x \sim v \forall v \in V$ and $\nexists w \in W$ with $x \sim w$ . The proof is constructive: let $x = v_t$ where $t = k \cdot 2^j + \sum_{v_i \in V} 2^i$ for $k$ and large enough $j$ both in $\mathbb{N}$ .

Induced subgraphs

Now we get our first impressive result. Every graph $G$ with $V(G)$ countable is an induced subgraph of $R$ . For, supposing the vertices of $G$ are labelled $g_0, g_1, g_2 \ldots$ , we require an injective function $f: V(G) \mapsto V(R)$ with $g_i \sim g_j \iff f(g_i) \sim f(g_j)$ . Let $f(g_0) = v_0$ as a base case, with the inductive hypothesis that $f$ defined on $g_0 \ldots g_n$ obeys the rule. Then for the inductive step we can find $f(g_{n+1}) \in R$ adjacent to precisely the correct vertices due to the extension property.

Uniqueness

Next things start to get weird, because it turns out that all countable graphs with the extension property are isomorphic. We will prove this by letting $R$ and $S$ be two rival countable graphs with the extension property, and finding $f$ an isomorphism between them. We label the vertices of $R$ and $S$ in the normal way and let $f(r_0) = s_0$ . Then supposing inductively that $f$ is legal and defined on $r_0 \ldots r_n$ , and $f^{-1}$ is defined on $s_0 \ldots s_n$ , we set values for $f(r_{n+1})$ and $f^{-1}(s_{n+1})$ using the extension property if they haven’t already been set. Hence $R \cong S$ . We can also start with an isomorphism between any two induced subgraphs of $R$ and build up the full isomorphism from there, so we find that the graph is symmetric and ultrahomogeneous.

That was quite momentous. You may have seen it coming, but just like global warming that doesn’t stop this from being a big deal. As a consequence the weirdness becomes endemic.

Damaging the graph

Suppose $R'$ is obtained from $R$ by deleting finitely many vertices and adding or deleting finitely many edges. Then $R \cong R'$ . This is a corollary of uniqueness; it is very easy to show that $R'$ has the extension property (notice that in the proof of the extension property $k$ can be any integer so there are infinitely many legal $x$ ).

That’s really weird. If the graph is subjected to GBH (or indeed initiated into a Cambridge drinking society) it retains its shape.

Tearing the graph into pieces

Equally weird is the following: If $V(R)$ is partitioned into finitely many subsets $A_1, A_2, A_3 \ldots$ then at least one of the corresponding induced subgraphs is isomorphic to $R$ . This follows immediately from the case of a partition into two sets. For sets $A$ and $B$ , suppose $A$ is not the Rado Graph. Then there are subsets $V_1, W_1 \subset A$ such that every $x$ extending $V_1, W_1$ is in $B$ . Now for any subsets $V_2, W_2 \subset B$ , there is an $x$ that extends $V_1 \bigcup V_2, W_1 \bigcup W_2$ , and $x \in B$ , so $B$ has the extension property. Hence either $A$ or $B \cong R$ , so in the general case, for some $k$ , $A_k \cong R$ .

Similarly, if the edges are $k$ -coloured for finite $k$ , then there exists an induced subgraph which is a 2-coloured Rado graph. The proof of this makes up the better part of a paper by Sauer and Pouzet which costs £30, so I won’t reproduce it here. However I will point out that this only needs to be proved for $k=3$ for the same reason as above.

The Random Graph

Perhaps you’re sufficiently weirded out already. Perhaps you’ve found all the weirdness so far rather run-of-the-mill. Either way, I think you’ll agree that the next realisation is about as weird as they come.

We start with an empty, countably infinite graph. We pick any $0 < p < 1$ and we go through each pair of vertices, constructing an edge between them with probability $p$ . The graph we get, independent of $p$ , is almost always (i.e. with probability 1) the Rado graph. This is actually easy to prove, using extension and uniqueness; for any set of vertices $V$ and $W$ , and some vertex $x$ not in $V$ or $W$ , the probability that $x \sim v \forall v \in V$ but $\nexists w \in W$ with $x \sim w$ is positive, so taken over all possible $x$ it is true with probability 1. Since $U$ and $V$ are finite, the number of pairs of subsets is countable, and the intersection of countably many events each with probability 1 is 1, as required.

At this point, the weirdness is so intense that it threatens to destroy the universe as we know it. Things fall apart at the seams. It turns out that the moon is made of cheese; China withdraws unilaterally from Tibet and voluntarily cedes all authority to Taipei. The Israeli government and the Palestinian Authority sign a peace treaty implementing a one-state solution, and the new country is known as the Federal Republic of Integral Bananas. Americans vote unilaterally to ban the ownership of firearms in a referendum, and scientists discover a cure for cancer whose active ingredient is powdered chocolate. Finally, every member of the IMO team gives up maths and enrols at Oxford for an undergraduate degree in History of Art. Why? Because the random graph on $\aleph_0$ vertices is in fact the not-very-random-at-all graph.

Alternative Constructions

Now that the Rado graph has ripped the universe apart it can sit back and just show off for a bit. Here are two alternative constructions of $R$ ; both can be verified using the extension property and are set as an exercise for the reader.

Let the vertex set be all primes $p \equiv 1 \pmod 4$ . Put $p \sim q \iff \left(\frac{p}{q}\right) = 1$ . To verify this you need to understand the basics of quadratic reciprocity and Dirichlet’s theorem.
Let $S \subset \mathbb{N}$ be universal; that is, writing $S$ as a string of 0s and 1s in the natural way, every finite string of 0s and 1s can be found in $S$ . Then let the vertex set be $\mathbb{Z}$ and put $a \sim b \iff |a-b| \in S$ . This one can be proved without any further knowledge.

Proving stuff about this graph is quite easy

Everything we’ve seen has been quite easy to prove. That’s what I like about the Rado graph; the definition is such that everything else just falls into place. To convince yourself of this, why not find a few simple properties of the Rado graph, such as its chromatic number, its diameter and its complement? Does there exist a Hamiltonian path through every vertex? In a cops and robbers game where the robber takes it in turns with n cops to move to an adjacent vertex (all the cops move at once), who wins? Everything seems to come straight out of the definition of the Rado graph.

Why you should adopt the Rado graph as your favourite graph

A favourite graph is most useful for testing hypotheses. As such, the Rado graph is an excellent choice of favourite graph because of three features that make it a good candidate for answering hypotheses in the negative. These are:

It is easy to work with. The immense symmetry, the extension property, the subgraph property and the uniqueness of the Rado graph make it very easy to prove things about it. Therefore it will ordinarily be easy to check whether a hypothesis is true for the Rado graph (see previous paragraph).
It has strange properties. This makes it feasible that the Rado graph should provide a much better answer to a problem than any other graph.
It is unusual. Suppose you were to bump into your friends as they struggle to prove or disprove some graph-theoretic hypothesis, and the Rado graph provides a counterexample. You can look forward to several minutes of sincere respect for such an elegant yet obscure solution. On the other hand, if your favourite graph is the complete graph on three vertices, and that provides a counterexample, then it’s probable that your friends will already have answered their hypothesis by the time you arrive. Moreover, if you are in time to use $K3$ as a counterexample, your solution will be met not with awe or respect, but with disappointment and embarrassment. The same goes for any exams; if a well-known counterexample exists, the hypothesis is unlikely to be set as a question, whereas it’s not unlikely that the Rado graph should provide a counterexample.

“But I’ve already got a favourite graph!”

I recognise that many people are already in a relationship with a graph, especially since those who were single a few weeks ago probably hooked up with the Petersen graph after being introduced to it by Adam. Nevertheless there are likely to be readers without one, either because they had a bad first date with the Petersen graph, or because they have broken up since then due to the inevitable disappointing relationship that followed those dream-like first few moments. Additionally, it’s probable that some readers didn’t see that post, in which case they might still be virgins. Finally, those in a relationship with the Petersen graph might be ready to move on; indeed, it is rather promiscuous (by which I mean overused), and just as any partner ought not to sleep around, so a favourite graph ought to be unusual. If, on the other hand, you are happily married to the Petersen graph, perhaps you might want to adopt the Rado graph as your favourite infinite graph. If the Petersen graph is insulted, remind it that the Rado graph contains infinitely many copies of the Petersen graph.

Sources

http://www.math.unt.edu/~mpc0061/logicgroup/randomgraph.pdf
http://en.wikipedia.org/wiki/Rado_graph
http://mabit.org.hu/~p_erdos/1963-04.pdf

Posted in Uncategorized | 10 Comments