Complex Projective 4-Space

We’re quickly approaching Ebenezer Scrooge’s favourite time of the year, Greenwich Mean Time. This brief post serves as a reminder to anyone who has forgotten about the temporal adjustment due to spending too little time in real Euclidean 3-space. Of course, if you, like Joseph Myers, have a radio-controlled watch, then there is absolutely no need to worry.

I’d like to thank everyone for the flurry of comments on the previous post. Amongst the posters was Erik Demaine, the youngest person to be accepted as a professor at MIT (at the age of just 20 years!).

Last, but by no means least, happy (integer!) birthday to Vishal. He requested a text-only version of the chess cipher, so I hope this suffices as a birthday present. If you would like your birthday mentioning on cp4space, let me know and I’ll make a note of it.

Update: I’ve repaired the broken link to the text-only chess cipher by placing it on pentadecathlon.com instead of Google Drive.

We’ll begin with an intriguing set of three interlinked rings, the Borromean rings. They can’t be realised as solid circular tori, but ellipses work just fine. Here is a visualisation:

If you remove any one of the three rings, the other two rings are unlinked. However, it is impossible to separate the rings without breaking one of them. Borromean rings have appeared in the structure of molecules, snakes and in heraldry. It turns out that its structure is equivalent to the standard three-strand braid, which likewise has the property that removing any one strand unlinks the remaining two. Here’s a picture from Wikipedia:

The Borromean string problem

On this topic, I propose the following group-theoretic puzzle:

Consider strings over the alphabet {a, b, c, a’, b’, c’}, where a’, b’ and c’ are the inverses of a, b and c, respectively. Formally, these strings are elements of the free group on three generators. Does there exist a string S with the following properties?

1. In the free group, S is not equivalent to the identity;
2. When all instances of any symbol and its inverse are removed (or, equivalently, by replacing that symbol with the identity), the string S is equivalent to the identity.

For example, a b a’ c a b’ a’ c’ is almost a ‘Borromean string’, since it works when b is removed or when c is removed:

• Removing b, we have a a’ c a a’ c’ = a a’ c c’ = c c’ = identity;
• Removing c, we have a b a’ a b’ a’ = a b b’ a’ = a a’ = identity;
• However, removing a gives b c b’ c’, which is not the identity, so it is not a Borromean string.

Feel free to discuss any progress/solutions you have in the ‘comments’ section below:

Shortly after publishing my third cipher, the second one (labyrinth) was solved by someone called Patrick. Gabriel had worked out the basis for solving the cipher ages ago, but didn’t actually do the necessary combination of brute-force frequency analysis to decipher it. I’m pleased that no-one cheated by using my Golly-compatible cellular automaton (which, I now suppose, you can run on the iPad implementation of Golly).

I don’t usually entertain requests, but since I had such a great time last night I’m willing to make an exception. Ben and Vishal asked for the next post to involve Markov music and underwater basket-weaving, respectively. My attempt to splice these two very disparate threads (no pun intended) forms the basis of this article.

Penney’s game

This is completely unrelated to the Cantabrigian tradition of dropping low denominations of British money into opponents’ beverages (it happened to me!), but is instead named after its creator, Lord Walter Penney. To relieve the monotony of their early retirement from the world of cryptography, Alice and Bob decide to play the following game:

• Alice selects some three-digit binary sequence of coin tosses, such as HHT.
• Bob follows by choosing a different three-digit binary sequence, such as THH.
• A coin is tossed repeatedly to generate a binary sequence. I’m going to actually do this now, forsaking the opportunity to make a pun on the name of the game and instead tossing a £2 coin bearing an excerpt from a quotation by Sir Isaac Newton. The resulting sequence was THTHH, whence the game terminated as Bob’s string appeared. Hence, Bob won that particular game.

So, what are the probabilities of each player winning? We can analyse this by something called a Markov chain. We only need to keep track of the current symbol and the previous two, so the analysis is quite straightforward. In the diagram below, a red edge corresponds to a head appearing, and vice-versa.

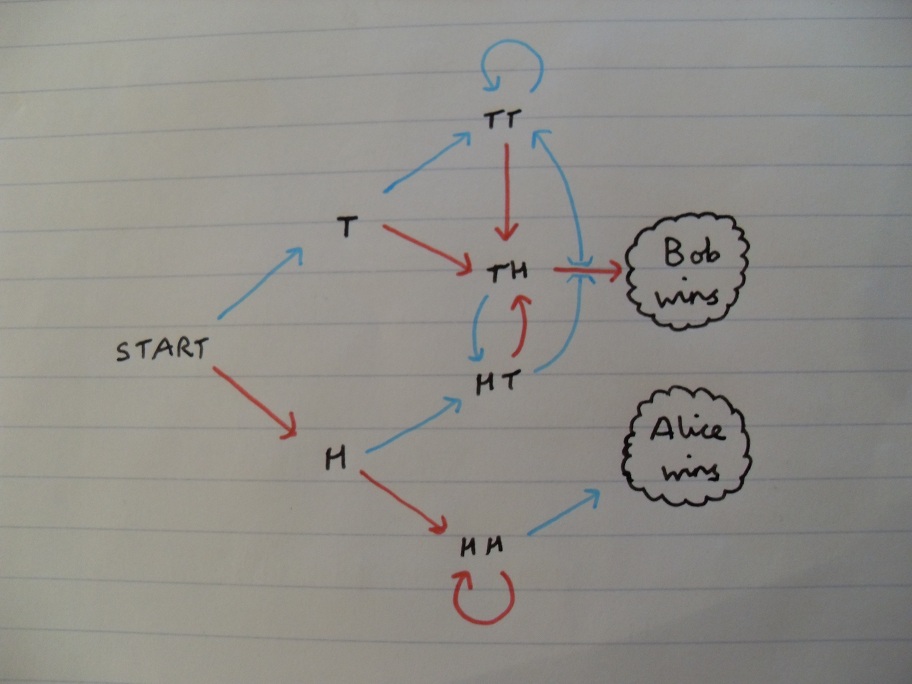
We can think of these as being pipes transferring liquid between various containers, where half of the liquid in each container moves down the red arrow, and the other half propagates along the blue arrow. This diagram is rather simple, since it splits into two non-interacting halves, one of which leads to Bob almost surely winning, and likewise for Alice. It is evident from the diagram that Bob wins 75% of games played.

It turns out that the game is non-transitive, and Bob can always guarantee at least a 66% success probability, irrespective of Alice’s initial choice.

Markov music

It is similarly possible to replace the letters with musical notes, and weight the probabilities according to how often a particular note follows another note in a piece of music. Then, by following the Markov chain randomly, we can create something that locally resembles the original piece of music.

There is a reason I embolded the word ‘locally’. Even though we have all the right intervals (a technical term for two adjacent notes and the space between them), they’re not necessarily in the right order! The resulting tune, although it could hypothetically be identical to the original music, is most probably an awful cacophany. Richard Freeland wrote a computer program to do precisely this, and these were indeed his findings. For a piece of music to be pleasing, it needs to have some global structure.

We can, however, refine the original technique by using a larger ‘memory’ than a single note (for example, an entire bar). This would make a brief sample of (say) three seconds of the random tune appear indistinguishable from the actual music. The larger the memory, the better the tune.

Underwater basket-weaving

In the same way a musician can read a score of music and produce a tune, the 200-year-old Jacquard loom reads punched cards detailing instructions to weave complex patterns. As for whether it could perform the somewhat Herculean labour of underwater basket-weaving remains to be seen. Nevertheless, we could generate the punched card by a Markov process so as to create a randomised basket.

To keep this firmly within the realms of mathematics, here is a woven basket in the shape of a dodecahedron.

Forgive me if there is a slight lapse in the frequency of CP4space postings. You can attribute it to me lying in the quintuple-intersection of the following Venn diagram:

This particular arrangement of ellipses partitioning the plane into 32 connected subsets was discovered by Branko Grunbaum, who you may recognise as one of the authors of Tilings and Patterns. There have been similarly symmetrical Venn diagrams discovered with seven and eleven sets, but they require much more convoluted curves than mere ellipses. The article claims that they can only exist for prime numbers of sets. I doubt this assertion, since the obvious argument (that n divides 2^n – 2, which follows from the symmetry of the configuration) does not rule out Fermat pseudoprimes such as 1729.

Speaking of symmetrical objects, there was some recent hype about hexaflexagons. They were originally mentioned in an article by Martin Gardner some years ago, then discussed ad nauseam in three videos by Vi Hart. If you didn’t already know, Vi Hart is one of a group of rebellious rapscallions attempting to overthrow accepted mathematical notation by using the symbol τ = 2π. (This reminds one of when Royal Mail wasted millions of pounds changing its name to Consignia, only to revert shortly afterwards.)

[youtube=http://www.youtube.com/watch?v=jG7vhMMXagQ]

Don’t let her attempt to convert you to Tauism with those Raspberry Pies! Instead, take a look at this much more delectable dessert I conceived earlier.

This, of course, was consumed months ago by a select group of really fortunate people. You may recognise it as an attempt to reconstruct the infamous Wolfson building, a monstrosity erected in the 1960s. It even comes with its own ‘suicide door’, which faces out of a second-floor window into thin air!

Yes, this actually exists. You may have noticed from the cake and the photograph that this building is an orthogonal polyhedron. If you haven’t heard the terminology before, it’s just a polyhedron where all incident edges are perpendicular. There are some nice combinatorial problems on this theme.

The plane partition problem

A plane partition is an orthogonal polyhedron composed of unit cubes, such that there are no empty spaces below, behind or to the left of each cube. For instance, this is a valid plane partition:

How many plane partitions can fit inside a cube of side length n? It is a remarkable fact that drawing it in the isometric projection actually converts it into a seemingly different problem. Here is the same polyhedron drawn inside the 3 × 3 × 3 cube (i.e. the case where n = 3).

On second glance, this is also a tiling of a hexagon of side length 3 with rhombi! Regarding each rhombus as the union of two triangles, this can be rephrased as a bipartite matching of the following grid of triangles:

Observe that the triangles are either ‘pointing left’ or ‘pointing right’, and adjacent triangles point in opposite directions. We will thus categorise the triangles into two sets, L and R. Observe also that there are equal numbers of rhombi of each colour. This will prove useful later on.

Form an adjacency matrix, where each row corresponds to a triangle in R and each column corresponds to a triangle in L. Each element of the matrix is either 1 (if the triangles corresponding to the row and column are adjacent) or 0 (otherwise). The determinant of this matrix counts the ways in which we can biject elements in L to elements in R, respecting adjacency. So, this determinant counts precisely the number of tilings of the hexagon with rhombi, and thus the number of plane partitions!

More things on this theme are described in this article by the AMS. For instance, the problem of finding domino tilings of a chessboard is solved almost identically.

Many natural objects can be modelled by startlingly simple equations. For instance, there is a sextic surface (degree-6 polynomial equation in three variables) which resembles a heart. As such, it has been nicknamed the ‘heart surface’:

Now that we’re approaching Hallowe’en, I decided to do a similar thing to create a pumpkin. Due to its approximate spherical shape, the spherical coordinate system seemed like a good idea. I then used trigonometric functions to create the undulations:

Similarly, a cylindrical coordinate system is perfect for modelling surfaces such as hats. This time, I attempted to recreate an infamous hat worn by certain students at the Part IA lectures in the Cambridge Mathematical Tripos:

If you can decipher the Mathematica code, you’ll see that the equation (in cylindrical coordinates) is z = (3/2) Exp[-r^4] + (1/12) r^2 Cos[3 theta]. This was derived by modifying the ordinary Gaussian distribution until it had the correct shape. The trigonometric term causes the rim of the hat to vary sinusoidally. I then coloured the hat depending on radius to give the appearance of the black band.

It is usual, in Cambridge, to hear a plethora of bells chiming. Being within hearing range of the chapels of both Trinity and King’s college, I am greeted with clocks chiming every quarter-hour.

On Sunday mornings, however, someone plays the entire full peal (or extent) on six bells. This involves ringing them in all 6! = 720 possible permutations, in sequence, to create a beautiful sound lasting for about half an hour. Here are the first few permutations:

Due to both aesthetic and practical considerations, however, not all of the (6!)! possible sequences of permutations are admissible. Generally, the following restrictive set of rules must be obeyed:

• Two adjacent permutations must be precisely one transposition (2-cycle) away from each other;
• This 2-cycle must permute two adjacent bells.

This ensures that the time delay between the same bell ringing twice is either 5, 6 or 7 intervals. The way that bell-ringers achieve this is to use the recursive Steinhaus-Johnson-Trotter algorithm. We begin with a valid sequence on n-1 bells, and extend it to a valid sequence on n bells. By induction from the trivial base case, this leads to sequences on any number of bells, including six.

The trivial base case is the single permutation of one bell. We replace every permutation on n-1 bells with n permutations on n bells. For example, the permutation {a,b,c,d} is replaced with:

• {a,b,c,d,e}
• {a,b,c,e,d}
• {a,b,e,c,d}
• {a,e,b,c,d}
• {e,a,b,c,d}

This is the same permutation with ‘e’ inserted at every possible position in order. For the next permutation, we reverse the positions where we insert the ‘e’. For instance, if the next permutation is {a,b,d,c}:

• {e,a,b,d,c}
• {a,e,b,d,c}
• {a,b,e,d,c}
• {a,b,d,e,c}
• {a,b,d,c,e}

It is clear to see why the algorithm works as intended. It is also a proof that every permutation can be reached by swapping adjacent elements, and thus that any 2-cycle together with any p-cycle generates the symmetric group S_p.

Similarly recursive algorithms are used to generate the sequence of moves for solving the Tower of Hanoi puzzle.

The Ready gang have been doing more experiments lately, and I ought to summarise the recent discoveries in reaction-diffusion systems. You may remember Robert Munafo’s ‘U-skate’ configuration, which propagates through space even when bombarded with radiation:

[youtube=http://www.youtube.com/watch?v=_sir7yMLvIo]

Well, lately Tim Hutton and Robert Munafo have collaborated to extend this work into three dimensions. The Munafo glider doesn’t function properly, but Tim realised it can be stabilised by adding three nearby spheres. The entire complex moves along its axis of symmetry. (Warning: these videos are on a toroidal grid, so configurations can appear to exit one face of the box and re-emerge from the opposite face.)

[youtube=http://www.youtube.com/watch?v=WYZVffOaRgA]

It is very sensitive to initial conditions. Drawing it incorrectly can cause the front to detach from the stabilising balls and twist in a double-helix, as Robert did inadvertently:

[youtube=http://www.youtube.com/watch?v=0Fp6v0m801g]

The story doesn’t end here. Robert added a fourth sphere to it, which still results in a functional glider. However, it breaks the symmetry, causing it to exhibit a rotational bias. This propels the glider in a helical path. Helical paths are also followed by flying insects with damaged wings, or indeed electrons in a uniform magnetic field.

[youtube=http://www.youtube.com/watch?v=B03lcPEmSOQ]

If you watch the video, you’ll see the regular and helical gliders bounce off of each other a couple of times before coalescing and cohering. The result itself moves even more chaotically than before. To return to the entomological analogy, try gluing two fruit flies together and watch how the complex moves*. I can guarantee it will resemble this video.

*Actually, don’t do it. Drosophila melanogasters have rights!

Interesting things can happen in two dimensions as well. Check out Tim Hutton’s video of SmoothLife, a continuous cellular automaton by Stephen Rafler:

[youtube=http://www.youtube.com/watch?v=KJe9H6qS82I]

The original program uses the Fast Fourier Transform to accelerate computation. This is not the time to discuss Fourier transforms and their applications, but I won’t object to you tentatively supposing that there might be a small probability that such a topic may later be considered for possible inclusion on cp4space. Don’t quote me on that, though.