Complex Projective 4-Space

I have returned from assisting at the Easter olympiad training camp at Trinity College, Cambridge. After we marked a selection test (the results of which I am not at liberty to divulge), a preliminary squad of nine people were selected, which will eventually be narrowed down to the six people that form the IMO team.

In addition to satisfying the role of General Dogsbody, I gave an unofficial talk on Ramsey theory at 7:00 am. Considering the early hour, lack of advertisement and the optional nature of the talk, the attendance (three people) was actually quite reasonable. I distributed a sheet of questions (PDF). If you wish to attempt them, I suggest familiarising yourself with the theorems in the third chapter (Combinatorics II) of MODA. Two of these were marked with a direct sum symbol () to indicate that they’re extremely challenging, and far beyond the hardest of IMO questions.

Another function of the Easter camp was to prepare our team of four girls for EGMO 2013, which was held in Luxembourg last week. The scores at the end of the competition were continually updated to a live online scoreboard, followed shortly after by the medal boundaries. Danielle Wang (USA) won the competition, with a total of 38 marks out of a possible 42. Three nations (Belarus, Serbia and the United States) were tied in equal first position, with cumulative scores of 99.

Solutions and commentary (spoiler alert!)

The problems appear to be arranged in strictly increasing order of how interesting they are, so I’ll only discuss the second paper here.

Problem 4: Quintic polynomial

This one isn’t actually particularly interesting; however, I’ll include it here for completeness, since it would seem strange to only discuss questions 5 and 6.

4. Find all ordered pairs of positive integers (a, b) for which there are three consecutive integers at which the polynomial takes integer values.

In problems such as this one, it is most convenient to let the three consecutive integers be {n − 1, n, n + 1}. Then, we require (n − 1)^5 + a, n^5 + a and (n − 1)^5 + a to all be divisible by b. Since is an ideal of , we can add multiples of b and multiply by integers whilst retaining divisibility by b. Consequently, the polynomials and must also be multiples of b.

Hence, b and n are coprime, and both  and  are divisible by b, so we can conclude (eventually) that . For the case where , all integer values of a trivially work. For the other case of , it suffices to consider the residues of n^5 (mod 11) to find all solutions for a.

Problem 5: Mixtilinear incircle

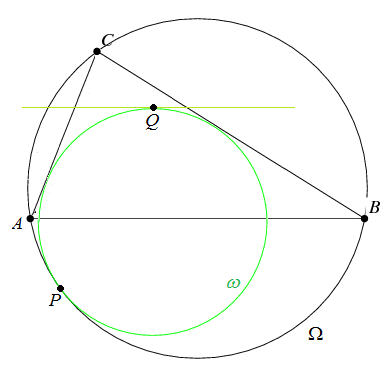
5. Let Ω be the circumcircle of ABC, and let ω be the mixtilinear incircle touching BC, AC and internally tangent to Ω at the point P. A line parallel to AB and intersecting the interior of triangle ABC is tangent to ω at the point Q. Prove that angles ACP and QCB are equal.

What makes this problem particularly appealing is that there are only five important points. In a situation like this, one would normally find a clever Euclidean construction involving additional points, or apply some algebraic bash. Quite remarkably, we can solve this problem without introducing any more points.

To solve this problem, we’ll use a Möbius transformation obtained by the composition of an inversion in a circle centred on C and orthogonal to ω followed by a reflection in the angle bisector of BCA. This is actually a natural thing to do, since lines through C remain as lines, the mixtilinear incircle ω is preserved, the circumcircle Ω is mapped to a line, and lines AC and BC are interchanged. Our Möbius transformation is an involution, although we don’t need this fact.

The image of Ω is the line A’B’, where A’ and B’ are the images of A and B. It shouldn’t be difficult to convince yourself that B’A’C is a homothetic copy of ABC, so A’B’ is parallel to AB. Also, A’B’ must be tangent to ω and intersect the interior of the triangle, so it is precisely the line used to construct Q. We can deduce, therefore, that P and Q are interchanged, whence it follows that angles ACP and QCB are indeed equal.

The Möbius transformation is colloquially referred to as an inverflection, being composed of an inversion in a circle followed by a reflection in a diameter of the circle. On the Riemann sphere, this operation is indistinguishable from a reflection in a point, which is why it is a natural thing to do. Sahl Khan applied this method to a difficult geometry problem on RMM 2011, and constructed several problems of his own relying on this principle.

Problem 6: Snow White and the Seven Dwarves

6. Snow White and the Seven Dwarves are living in their house in the forest. On each of 16 consecutive days, some of the dwarves worked in the diamond mine while the remaining dwarves collected berries in the forest. No dwarf performed both types of work on the same day. On any two different (not necessarily consecutive) days, at least three dwarves each performed both types of work. Further, on the first day, all seven dwarves worked in the diamond mine. Prove that, on one of these 16 days, all seven dwarves were collecting berries.

This is a thinly-veiled problem asking for you to essentially prove that the Hamming(7,4) code is optimal and unique. Its optimality follows from it being a perfect code; specifically, each of the 128 binary strings of seven digits is within a Hamming distance of 1 from precisely one of the 16 codewords.

Uniqueness is slightly more difficult. We are given that 0000000 is a codeword, and want to show that 1111111 is also a codeword. This must be a perfect code (essentially a space-filling sphere packing on the Boolean lattice), which means that every binary string must either be a codeword or differ from precisely one codeword in a single position. Consequently, every string of Hamming weight 2 (such as 1100000, 0010100 and 0001001) must differ from a codeword of Hamming weight 3 in a single position.

Essentially, we want to group the seven dwarves into overlapping ‘lines’ of three dwarves, such that any pair of dwarves determines a unique line. From this, we can deduce that each dwarf belongs to three lines, and thus there are seven lines (corresponding to codewords of Hamming weight 3). This describes the Fano plane, as Maria Holdcroft noticed when attempting this problem in the actual competition:

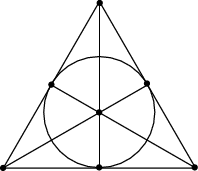
If the problem is false (i.e. 1111111 is not a codeword), then we must have a codeword of Hamming weight six. Without loss of generality, this is 0111111, and three of the other codewords are 1110000, 1001100 and 1000011. Now consider the string 0001111. This can’t be a codeword (since it differs from 0111111 in only two positions), so must differ from a codeword X in one position. Clearly, X cannot be 0101111 or 0011111 (since then it would be too close to 0111111). It can’t be 1001111 either, as that is too close to 1000011. Hence, X must be either 0001110, 0001101, 0001011 or 0000111. The first two ‘collide’ with 1001100; the last two collide with 1000011. Hence we obtain a contradiction, and our proof is complete.

A more difficult generalisation of this problem involves 23 dwarves who work for 4096 days, such that for any two days, at least 7 dwarves do different types of work. The unique solution is then given by the perfect binary Golay code.

Hall’s marriage theorem is well-known and frequently useful, but it’s a nightmare from a computational perspective.

The standard proof can be turned into an algorithm which finds a matching, but it’s impracticably slow. The reason for this is that the theorem contains the phrase “every subset”, and one doesn’t want to be testing every subset of a set in real life. Indeed, an algorithm that matches n men to n women in time is in some sense not much better than trying every possible matching in turn!

But, as it turns out, there’s another way of going about the subject which is much more efficient in practice: an approach apparently well-known to experts, but not well-known to one of the authors (JDC) until last week.

We’ll need the notion of a partial matching: that’s when we have some marriages, and perhaps some unmarried people left over. Ignoring civil partnerships, bigamy, trigamy, and all higher-order polygamy, real life is a partial matching; the concept is familiar.

Given a partial matching, we’ll say that a swingers’ party is a line of people with the following properties:

• there are an even number of people (at least two);
• they alternate between men and women;
• the people at each end are unmarried (wlog, a man on the left and a woman on the right);
• the people between the ends are a chain of married couples;
• every pair of neighbours in the line wouldn’t mind being married.

In other words, it alternates between couples who simply fancy each other, and couples who are already married:

Note that there is a degenerate case, consisting of two people: one unmarried man and one unmarried woman who would be happy to be married. Conventional morality frowns strongly upon unmarried men being alone at parties with unmarried women, so we do not mind calling this degeneration a swingers’ party.

However, in a striking departure from conventional morality, swingers’ parties are a great thing for improving matchings. If you can find a swingers’ party, you can swap over the married couples and the unmarried couples, and that increases the number of marriages by one.

The theorem of interest is that a configuration admits a total matching if and only if, given every partial matching, and any unmarried person, we could hold a swingers’ party featuring that person. In fact it’s enough to have this true for any unmarried man, or alternatively for any unmarried woman.

If we have an incomplete matching with no potential swingers’ parties, then we can find a set which violates Hall’s marriage condition. Specifically, we choose an unmarried man, together with all the women whom he fancies, and all of their husbands, and so on until we can go no further. This cannot terminate in an unmarried woman, lest we would have a swingers’ party. Hence, the resulting set must necessarily contain a surplus of men, violating the marriage condition and thereby proving that Hall’s condition implies that every incomplete matching contains a potential swingers’ party. The converse is trivial, so this is equivalent to the existence of a perfect matching.

What’s more, this theorem leads to a genuinely efficient algorithm. Given a partial matching and a choice of unmarried man, we can construct a swingers’ party in time linear in the number of potential marriages, if one exists, by searching in the obvious way and keeping track of dead ends. That means that, starting from the empty partial matching, with everybody unmarried, one can produce a total matching (if one exists) in time (and less if the number of potential marriages is bounded somehow), which is a considerable improvement.

In the literature, swingers’ parties seem to go by the euphemism alternating paths, but our instinct is to call them what they are.

(This post is a joint effort with James Cranch. Both authors wish to apologise for the inherent heteronormativity of the subject matter, and would love to hear about theorems which reflect reality better.)

The ordinary game of Noughts and Crosses, also known as Tic-tac-toe, features a board on which two players alternate placing symbols (O for the first player, and X for the second player) in unoccupied squares, attempting to form a line of three collinear squares containing their symbol. It has been known since time immemorial that, assuming perfect play, the game results in a draw. Randall Munroe provided a beautiful illustration of the optimal strategy for each player.

There have been extensions to higher dimensions. For example, a popular variant involves a board, where the first player to obtain four collinear cubes of their symbol wins. Apparently, this one is a victory for the first player (assuming perfect play), although humans play sufficiently suboptimally that this has no impact.

After receiving a particular text message ending with an alternating string of ‘X’s and ‘O’s, I was inspired to go in the opposite direction and consider variants of Noughts and Crosses on a one-dimensional board. One particularly interesting example is a game mentioned on the Advanced Mentoring Scheme:

Two players (Alice and Bob) alternate placing either an ‘X’ or an ‘O’ on an unoccupied square of a board. As soon as three adjacent squares form the string ‘XOX’, the player who has just placed that symbol wins. If the board fills up without this happening, the game is declared a draw.

It’s relatively easy to show that the only losing positions are those where the unoccupied squares form the string ‘X__X’, where placing either of the symbols in one of the empty spaces enables the opponent to secure an immediate win. Since losing positions must have an even number of empty spaces, we can prove that Alice can force at least a draw for odd n, and Bob can force at least a draw for even n.

To force a win, the favoured player must therefore simply attempt to form the string ‘X__X’ and then play naturally, knowing that parity will eventually reward him or her with a victory. If the board is sufficiently large, it is easy to see that a win is guaranteed. The thresholds for forcing a win are n = 7 for Alice and n = 18 for Bob, far below the n = 2010 in the AMS question.

The Gamma function, Γ, is an extension of the factorial function to the complex plane. Specifically, Γ(n) = (n−1)! for all positive integers n. It is defined, more generally, by analytic continuation of the following integral, which converges for all complex numbers with positive real part:

The factorial identity can be verified using integration by parts. Specifically, we get the recurrence relation Γ(z+1) = z Γ(z). Plotting the absolute value of the function in the complex plane yields the following surface, with poles situated at zero and the negative integers:

At certain non-integer arguments, we get new irrational constants. For example, Γ(1/2) is the square-root of π. Γ(1/4) is even more interesting, and has been shown (by Yuri Nesterenko, in 1996) to be algebraically independent of both π and e^π; in other words, there is no non-trivial polynomial in π, e^π and Γ(1/4) with integer coefficients that evaluates to zero.

Also, we have , where S is the arc length of the lemniscate (shown above) given by the equation (and, of course, is our favourite transcendental constant). The area bounded by the curve is precisely 1, otherwise known as Legendre’s constant.

Related to this is Gauss’s constant:

AGM is the arithmetic-geometric mean, which is obtained by repeatedly iterating the map (x, y) → (√(xy), ½(x + y)) and taking the limit. There is an algorithm (the Brent-Salamin method) for calculating pi based on the arithmetic-geometric mean. The AGM converges extremely quickly, producing exponentially many digits of precision after n iterations. Nevertheless, the slower Chudnovsky algorithm is preferred for computing pi, due to the inefficiency of computing square roots.

Professor Sir Timothy Gowers FRS wrote about the usefulness of a particular proof strategy, known as ‘just do it’. He gives six example problems, providing proofs using this technique. I’ll now give alternative proofs, which use explicit constructions to avoid this idea completely.

Problem 1: Dense set in general linear position

The first problem is to find a dense subset of the plane, where no three points are collinear. We take z = (π + exp(π) i)/24, and let S be the set of all finite sums of distinct integral (both positive and negative) powers of z. For instance, S contains z^8 + z^79 and 1/z, but not 3z^3 or −z^2.

S contains no three collinear points, as otherwise we would have an algebraic relation between π and exp(π). Specifically, if a, b and c are collinear, consider a − b and a − c, where a has largest (or equal-largest) degree when viewed as a polynomial in z. They must be real scalar multiples of each other, i.e. Im((a − b)(a* − c*)) = 0. By the algebraic independence of z and z*, this means that (a − b)(a* − c*) must be a symmetric polynomial in z and z*. Considering the term of leading degree, a must have strictly higher degree (say, n) than both b and c. Now considering the terms divisible by either z^n or (z*)^n, we can deduce that b = c, so they are the same point.

S is dense, as we can easily show (by induction, or whatever) that every sufficiently large disc contains a point of S, and S is self-similar by definition. So we are done.

Points corresponding to sums of powers of z with degree between 1 and 14.

Problem 2: AP-free colouring of the integers

Is it possible to colour the positive integers with two colours, such that no arithmetic progression is either entirely red or entirely blue? Yes, we can. For example, colour the integer n according to the parity of the integer part of . For each colour, we get arbitrarily thick ‘bands’ that must contain terms of any given arithmetic progression.

Wow, that was really trivial. Much less involved than enumerating arithmetic progressions. If we replaced ‘arithmetic progression’ with ‘infinite recursively-enumerable set’, then the ‘just do it’ method is arguably better.

Problem 3: Packing spheres on the Boolean lattice

This asks for a collection of exponentially many subsets of {1, 2, 3, …, N}, such that the symmetric difference between any two elements of the collection is at least N/3. For N = 24, the binary Golay code is a beautiful example: there are 2^(N/2) = 4096 codewords, and the symmetric difference of any two of them has size 8, 12, 16 or 24.

A generalisation to arbitrary lengths is the notion of a lexicographic code, or lexicode. To construct a lexicode for this problem, we choose the lexicographically least subset of {1, 2, 3, …, N} which differs from existing subsets in at least N/3 positions, and continue until we cannot find any further subsets with this property. This construction necessarily works for the same reasons as Gowers’ ‘just do it’ approach. Lexicodes are also (entirely non-obviously) linear, which means that the symmetric difference of any two sets in the collection is also in the collection.

Problem 4: Finding a transcendental number

Liouville demonstrated that the number 0.11000100000000000000000100…, whose decimal representation is the indicator function of the set {1, 2, 6, 24, 120, …}, is transcendental. Naturally, the proof is a reductio ad absurdum, supposing that there’s a polynomial that vanishes at Liouville’s number.

Problem 5: Infinite matrix whose rows tend to 0, but whose columns tend to 1

This is really trivial. Merely extend the following matrix in the obvious way:

Problem 6: Every distance occurs once

The final of Tim Gowers’ questions is this: “Does there exist a subset Z of the plane such that for every positive real r, there is precisely one pair of points such that ?” He provides a non-constructive proof using transfinite induction up to the initial ordinal with the cardinality of the reals. I’ll leave the ‘don’t do it’ proof as an exercise to the reader…

Assuming everything has gone to plan, I am now introducing myself at the British Mathematical Olympiad training camp at Trinity. I’ll be assisting the future IMO team by making tea and providing biscuits (integral, if somewhat overlooked, roles in the administration of the camp), marking selection tests and promoting the use of transfinite induction, Muirhead’s inequality, and poles and polars.

Suffice it to say, I won’t have internet access for the next few days. As such, the posts you’re viewing have been written by me several days before, and have been set to automatically appear at predetermined times.

The British RMM team, and one of the guides. From left: Andrew, Silvia, Gabriel, Sahl, Daniel, Warren and Matei.

Also on the topic of UK olympiad training, Matei Mandache has written a very readable report about his experiences in the sixth Romanian Masters of Mathematics (whence the above photograph was taken). He has continued the very admirable tradition of mentioning me in student reports of competitions in which I didn’t compete.

I would, however, like to mention a single erratum (even if it may seem hypocritical, with my own report containing such howlers as ‘IMO stationary’ and ‘the Delhi Brassiere’!). Where he says ‘as they plan to be guides again, there is a good chance Gabriel or Warren will see them again, but for the rest of us the goodbye is final’, I have to disagree. At least one of the guides is intending to matriculate at Cambridge. Rather in the style of Douglas Adams, who didn’t immediately reveal who bruised his or her upper arm in The Hitchhiker’s Guide to the Galaxy, I shall not reveal to which of the four guides I am referring, thereby retaining an element of suspense…

If you’ve been affected by any of the issues in this post, you may want to take a look at MODA.