Complex Projective 4-Space

I overheard mention of a particular problem on a recent British Mathematical Olympiad, namely the following:

A number written in base 10 is a string of 3^2013 digit 3s. No other digit appears. Find the highest power of 3 which divides this number.

Personally, I bemoan such problems that are trivialised by the knowledge of advanced theorems, as it enables competitors to gain an unfair advantage by rote-learning many results rather than demonstrating creative mathematical thought. In this case, the question is trivialised by a rather elegant but little-known lemma called lifting the exponent.

So, what does the lemma state? Firstly, we establish the following definition:

Definition: the p-adic valuation v_p(n) of an integer n to be the highest power of p which divides n. For example, v_2(40) = 3, since 2^3 divides 40 but 2^4 does not.

Then the lemma is as follows:

Theorem (lifting the exponent): Let p be an odd prime, and a and b integers such that neither a nor b is divisible by p, but p divides their difference a − b. Then v_p(a^n − b^n) = v_p(a − b) + v_p(n).

Why is this true? The idea is that we factorise a^n − b^n like so, where n = k p^m and k is not divisible by p:

The factors in the final factorisation are highlighted. It is clear that it is sufficient to prove that the yellow factor is coprime to p (which is easy, since all of the terms are congruent modulo p and are non-zero) and each of the blue factors are divisible by p (easy for the same reason) but not by p², as we shall prove:

• If a and b are congruent modulo p², this is again trivial for the same reason as before.
• Otherwise, we have to actually rely on the property that p is odd (if p = 2, we need a and b to be congruent modulo 4 rather than modulo 2). We let x and y be equal to a^p^i and b^p^i, respectively, for the obvious value of i, such that the factor is of the form:

Γ = x^(p-1) + x^(p-2) y + x^(p-3) y^2 + … + y^(p-1)

Then we set y = x + lp for some integer l (which we can do, since y and x are clearly congruent modulo p). Expand the factor Γ to produce a sum of binomial expansions; we can ignore all terms of order p² and higher since we’re only interested in the residue modulo p². This gives the following expression:

The rightmost term vanishes, leaving something that is clearly not divisible by p². Consequently, the proof is complete and the result follows immediately.

Zsigmondy’s theorem

Another useful fact concerning a^n − b^n is this: except in a few exceptional cases, it has a new prime factor p that does not occur in any of a − b, a² − b², a³ − b³, …, a^(n−1) − b^(n−1). The exceptions to the rule are the following:

• a = 2, b = 1, n = 6: we have 2^6 − 1^6 = 63, whose prime factors are 3 and 7, which occur in 2^2 − 1^2 and 2^3 − 1^3, respectively.
• a + b is a power of 2, and n = 2: then a² − b² = (a + b)(a − b). The first factor is a power of 2 (so no new primes there), and the second factor is itself the previous term in the sequence (so, by definition, no new primes there either).

A related statement about Fibonacci numbers (where the integers a and b are replaced with irrational algebraic integers, and an extra factor of √5 slips in) is known as Carmichael’s theorem. Zsigmondy’s theorem and Carmichael’s theorem can be mutually generalised to other Lucas sequences.

Firstly, I have a few late items of news to discuss:

• Maria Holdcroft (former UK EGMO team member) and I survived our skydive on Wednesday, and have so far raised in excess of £886.77 (a large portion of which is from cp4space readers!) for the Schistosomiasis Control Initiative. A video of the freefall component of my jump is available; you may also want to visit the Facebook page. I’ll be writing the cheque to the SCI imminently, so if you want to support the cause (saving children in Africa from parasitic infections) then please e-mail me as soon as possible. If you happen to enjoy watching people jump out of aeroplanes, then you may want to watch this video of my friend Mehr, who partially inspired me.
• Today we marked the First Selection Test to decide the preliminary UK IMO squad who will be attending further training sessions in Oundle. The team for the Balkan Mathematical Olympiad will also be announced shortly on Joseph Myers’ website, but until then I’m sworn to secrecy. Congratulations, nonetheless, to our newly-appointed squad of Joe Benton, Gabriel Gendler, Frank Han, Liam Hughes, Freddie Illingworth, Andrew Kenyon-Roberts, Warren Li, Neel Nanda and Harvey Yau for their excellent performance in the selection tests, and good luck in South Africa.
• Also, I would like to draw attention to the final of University Challenge between Trinity College, Cambridge, and Somerville College, Oxford. As with the results of the IMO selection tests, I shall not reveal the scores…

Anyway, I suppose I should provide a cipher since we are rapidly approaching a Tuesday in the middle of Season III.

The password is eight letters long.

Niccolo Fontana Tartaglia, whom you may recognise from having discovered Cardano’s solution to the general cubic equation, also discovered a generalisation of Heron’s formula to compute the volume of a tetrahedron:

As you may expect, this can be generalised to compute the volume of any n-simplex (n = 2 reducing to Heron’s formula for the area of a triangle). I wondered how one would go about proving this identity, and then realised it can be accomplished by elementary facts about determinants. Firstly, it is easy to show the following result:

• The volume of an n-simplex S with vertices at {0, e_1, …, e_n} is equal to 1/n!, where e_i is the ith standard basis vector.

This can be proved, for instance, by subdividing a unit cube into n! simplices, each of which is congruent to S. Now, we know that the determinant of a matrix gives the volume scale factor of the associated linear transformation, enabling us to generalise the previous result:

• The volume of an n-simplex T with vertices at {0, a_1, …, a_n} is equal to V = det(a_1, …, a_n)/n! where we form the matrix by writing down the coordinates of a_i in the ith column.

Recall that determinants are multiplicative, so we can multiply this by its transpose to get the following equation (which is satisfyingly coordinate-independent):

• V² = (det R)/((n!)²), where the entries of R are given by Rij = a_i · a_j.

And then by scaling, we obtain:

• V² = (det Q)/((−2)^n (n!)²), where the entries of Q are given by Qij = −2 a_i · a_j.

This in turn leads to the following:

• V² = (det P)/((−2)^(n+1) (n!)²), where P (an n + 2 by n + 2 matrix) is obtained by taking the matrix Q and appending two useless ‘1’s (whose only affect is to negate the determinant) to the diagonal like so:

Now, we want to apply determinant-preserving elementary row operations to convert the Cayley-Menger matrix M given at the beginning of the article into the matrix P. Perform the following operations in succession:

• Subtract the 1st row from the 2nd, 3rd, …, (n+1)th rows;
• Subtract appropriate multiples of the final column from the other columns so that the first row is (0, 0, 0, …, 0, 1);
• Subtract the 1st column from the 2nd, 3rd, …, (n+1)th columns;
• Subtract appropriate multiples of the final row from the other rows so that the first column is (0, 0, 0, …, 0, 1).

Then it is easy to verify that the result is equal to P, by expanding each entry in terms of dot products.

Applications of the Cayley-Menger determinant

• The Cayley-Menger determinant is beautiful in its own right, expressing the squared volume of a tetrahedron solely as a polynomial in the squared edge lengths. Similar results hold for other polyhedra, which was a necessary component in establishing the Bellows Conjecture.
• If we form the Cayley-Menger determinant of five nearby points in general linear position in three-dimensional space, it will allow one to deduce whether the local Gaussian curvature is positive, zero or negative. This is described in more detail here.
• Several other theorems in distance geometry follow as special cases, such as Stewart’s theorem.
• The distances between atoms are determined by the bond lengths, so the shapes of certain molecules can be predicted using distance geometry.

Until very recently, the densest known packing of pound coins in the plane was the hexagonal lattice packing of circles, which achieves a density of π/√12 ≈ 0.9069. This was proved by Axel Thue to be the densest arrangement of points subject to the constraint that the minimum distance between any pair of points is d.

However, recently a new method of packing pound coins has been realised, which attains a marginally increased density of 4√3 − 6 ≈ 0.9282. Specifically, we take the following packing of dodecagons induced by the truncated hexagonal tiling:

This increased density is a consequence of a new dodecagonal pound coin being introduced, and not that there is a denser packing of circles (which is, of course, impossible). The coin has been designed on the basis that it is considerably more difficult to forge, and rather satisfyingly still includes one of the earliest anti-counterfeiting precautions: Isaac Newton’s milled edge.

Apparently there is a competition to decide the obverse design of the coin; maybe we could deliberately design and submit something with an even more subtle fundamental flaw than the famous gear train parity error of the two pound coin? It would be absolutely hilarious if we manage this. I feel that an overbalanced wheel or other perpetual motion machine would be too obvious, but an impossible cube with a portcullis on one face might just get past the quality control process…

(This is also the first recent British coin to lack a constant diameter, and will therefore necessitate a major overhaul of all coin-recognising machines.)

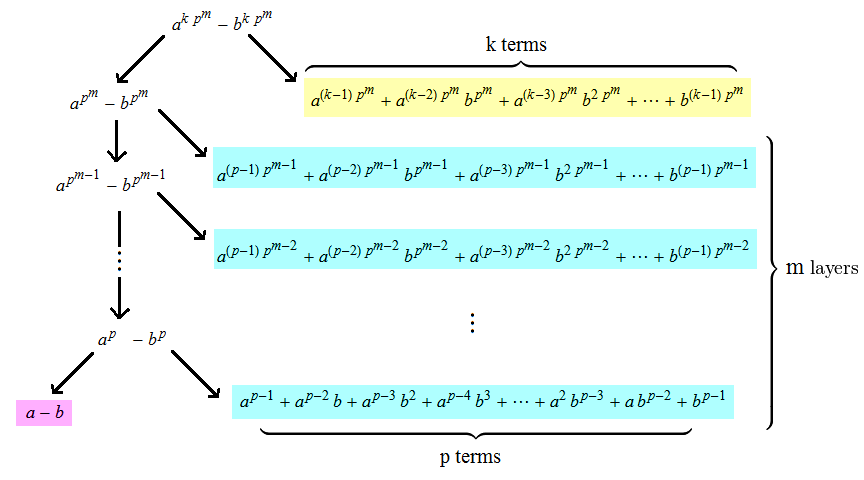
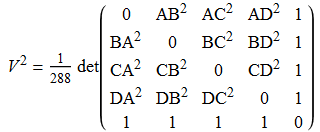
Firstly, a major announcement: Maria Holdcroft (whom you may remember from the cipher solvers page) and I will be performing a charity skydive on the 2nd April! If you wish to sponsor us, please specify the amount you intend to donate by commenting either on the Facebook event page xor at the bottom of this article. All donations will go entirely to the remarkably-efficient Schistosomiasis Control Initiative (which saves approximately one life per £0.50 GBP or $0.83 USD).

Anyway, without further ado, let us begin:

The orthocentre

In an arbitrary triangle ABC, the orthocentre H is the unique intersection point of the three altitudes (lines passing through one vertex and perpendicular to the opposite side). This is unsatisfactory as a definition, since we haven’t yet proved that the point exists. However, it is perfectly valid to define the orthocentre as such:

The orthocentre is the intersection of the altitudes from A and B.

Consequently, it is the unique point H such that AH is perpendicular to BC, and BH is perpendicular to AC.

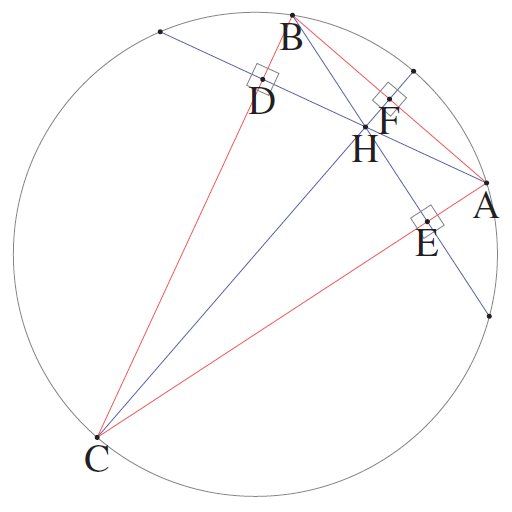
We wish to prove that CH is perpendicular to AB. There is a rather short proof using synthetic Euclidean geometry, although it’s rather boring. Instead, we can use algebraic projective geometry to prove the following more general statement, and then recover the concurrency of the altitudes as an immediate corollary:

A conic passing through A, B and C is a rectangular hyperbola if and only if it also passes through H.

Note that we adopt the convention that a pair of perpendicular lines is a (degenerate) rectangular hyperbola, so the lines CH and AB are perpendicular if and only if they together constitute a rectangular hyperbola.

Parametrising conics

We shall use projective coordinates, so the point with Cartesian coordinates (x, y) will have projective coordinates (x, y, 1). Moreover, the points (x, y, z) and (λx, λy, λz) are equivalent for all non-zero reals λ. Then, a general conic is an equation of the form:

• Γ(x, y, z) = Ax² + Bxy + Cy² + Dxz + Eyz + Fz² = 0

where A, B, C, D, E, F are not all zero. A conic is degenerate if it can be factorised into two linear terms, in which case it is the union of the corresponding lines. If A, B and C are all zero, then the equation z = 0 (the line at infinity) is a factor.

We can think of these equations as vectors (A, B, C, D, E, F) in a six-dimensional vector space. Scalar multiples of a given vector all represent the same curve, so the space of conics is actually a five-dimensional projective space. However, it is more convenient to work in the vector space than the projective space since we have extra structure, namely the operations of addition and scalar multiplication.

Observe that for any point P = (x, y, z), the constraint ‘the conic passes through P’ is a linear equation in A, B, C, D, E, F. Hence, the pencil of conics passing through a given point form a five-dimensional vector subspace (or a four-dimensional projective space of curves).

Consequently, the space of conics passing through A, B, C and H is a two-dimensional vector subspace. We would like to show that the space of rectangular hyperbolae passing through A, B and C is also a two-dimensional vector subspace, which would follow from being able to express ‘the conic is a rectangular hyperbola’ as a linear equation in A, B, C, D, E, F.

A rectangular hyperbola is defined to be a hyperbola whose asymptotes are perpendicular. Since we only care about the direction of the asymptotes, we can determine whether a hyperbola is rectangular simply by where it meets the line at infinity z = 0. Consequently, it suffices to throw away any terms containing a z, so we get a simpler ‘asymptotic’ equation of the conic:

Γ(x, y, 0) = Ax² + Bxy + Cy² = 0

If we express this as a product of two lines through the origin, (Px + Qy)(Rx + Sy) = 0, then the perpendicularity of the two lines means that P/Q = -S/R, or PR + QS = 0. Expanding out, this translates to the very simple linear condition A + C = 0. Consequently, rectangular hyperbolae through A, B and C indeed form a two-dimensional vector subspace.

However, we don’t yet know that they form the same two-dimensional vector subspace as the conics passing through A, B, C and H. To prove that, it would be sufficient to find two common ‘basis vectors’ — linearly independent rectangular hyperbolae that pass through A, B, C and H. But this is easy:

• The pair of lines AH and BC are perpendicular thus constitute a rectangular hyperbola;
• The pair of lines BH and AC are similarly perpendicular.

They are clearly different conics, so the equations are not scalar multiples of each other and therefore are linearly independent. This completes the proof.

A relevant fact is that the locus of centres of the hyperbolae passing through A, B, C and H is the nine-point circle of ABC. Again, with the machinery in place, this is not too difficult to prove. The centre of the conic is the point such that ∂Γ/∂x = ∂Γ/∂y = 0, so it is the intersection of the lines 2Ax + By + Dz = 0 and Bx + 2Cy + Ez = 0.

Since A + C = 0, it is easy to see that the two aforementioned lines are perpendicular. Also, the linear equations in A, B, C, D, E, F mean that each of the two families of lines (as the hyperbola varies) have a common point. Consequently, we can describe the locus of centres of hyperbolae as the locus of intersections of lines l1 and l2 such that l1 passes through P1, l2 passes through P2, and l1 is perpendicular to l2. We know by Thales’ theorem that this describes a circle.

It is now trivial to see that this must be the nine-point circle, since the three degenerate rectangular hyperbolae have centres given by each of the three altitude feet, and the nine-point circle is the unique circle passing through these three feet.

Interesting examples of such hyperbolae

Recall that five points in general position determine a conic, since they correspond to five linearly independent constraints and thus fix a one-dimensional subspace (which contains a single conic). Hence, if we specify a fifth point in addition to A, B, C and H, we get a unique rectangular hyperbola. This is particularly interesting when the fifth point is a triangle centre. Examples include:

• Kiepert hyperbola: also passes through the centroid G, the Spieker centre, the Fermat-Torricelli points, inter alia;
• Jerabek hyperbola: also passes through the circumcentre O and symmedian point K;
• Feuerbach hyperbola: also passes through the incentre I, Nagel point, Gergonne point and mittenpunkt.