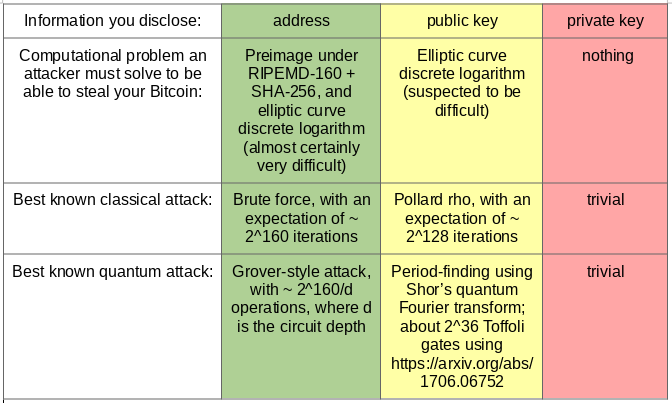
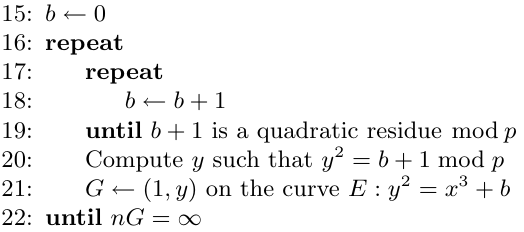One-way permutations are fascinating functions that possess a paradoxical pair of properties. They are efficiently computable functions φ from [n] := {0, 1, …, n−1} to itself that are:
- Mathematically invertible, meaning that φ is a bijection;
- Cryptographically uninvertible, meaning that it’s computationally infeasible in general to compute x given φ(x).
We’ll discuss a couple of constructions of one-way permutations. The first construction is simpler to understand, but is less secure (for a given size of n) or less efficient (for a given security level).
Construction I: using modular arithmetic
Let p be a large Sophie Germain prime; that is to say, a prime such that q = 2p + 1 is also prime. Then the field has a cyclic multiplicative group of 2p elements, and we can find a generator g for this multiplicative group.
Letting n = q − 1 = 2p, we can define a one-way permutation from [n] to itself as follows:
φ(x) := g^x − 1
The function g^x is a bijection from [n] to the set of nonzero elements modulo q, and the offset of − 1 maps this back to the interval [n]. It is easy to compute in the forward direction, by repeated squaring, but is intractible to invert when n is sufficiently large. The problem of inverting modular exponentiation is the discrete logarithm problem, and the largest safe prime for which this problem has been broken is 768 bits long.
To achieve a security level of 128 bits, NIST recommends using a 3072-bit value of n. The reason that this is so large is because the discrete logarithm problem is susceptible to index calculus attacks.
Attempting to use elliptic curves
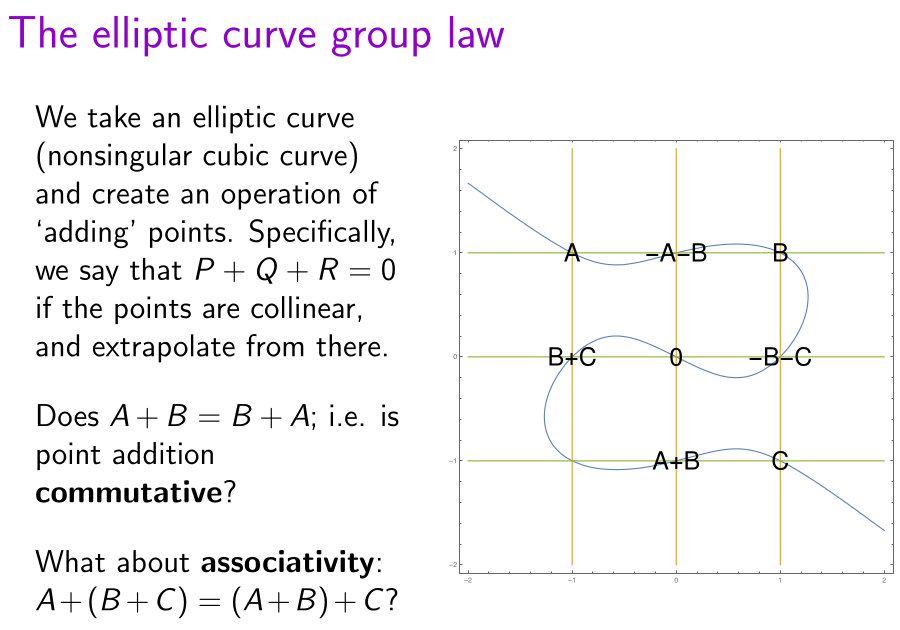
Recall that an elliptic curve is a nonsingular cubic algebraic curve. By using an appropriate change of variables, it can be written in the Weierstrass normal form as the equation y² = x³ + ax + b, where the nonsingularity condition is equivalent to the constraint that the discriminant 4a³ + 27b² is nonzero.
Elliptic curves admit a group operation. Specifically, to add two points A and B, do the following:
- draw a line through A and B, and let it intersect the curve again at C;
- draw a line through C and the point at infinity, and let it intersect the curve again at another point (A+B).
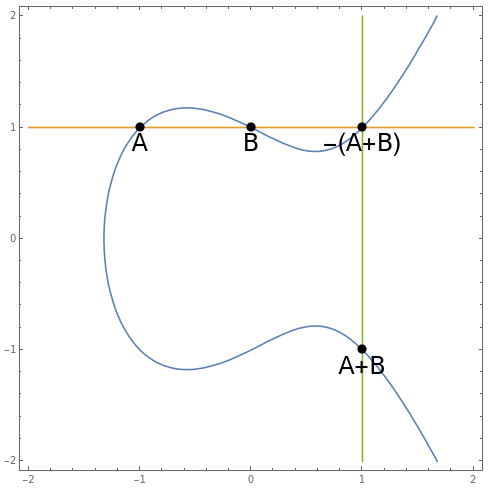
This operation is manifestly commutative, has an identity (the point at infinity), and admits inverses. The operation is also associative; as mentioned before, this can be proved using Cayley-Bacharach.
In cryptography, it’s customary to work with elliptic curves over finite fields such as . A theorem of Hasse states that the number |E| of points on the elliptic curve E is approximately equal to p, differing by O(sqrt(p)). Particularly useful is when the group of points on the curve is cyclic (a sufficient condition is for |E| to be squarefree), as then we can find a generator point G and formulate an analogue of the discrete logarithm problem.
For a given group size, the elliptic curve discrete logarithm problem is more difficult than the ordinary discrete logarithm problem, since for general elliptic curves there are no known algorithms faster than the Pollard rho algorithm. Note that some curves are much less secure than others; Daniel J. Bernstein has a website recommending how to choose a good curve.
Instead of the group size of 2^3072 recommended for NIST to provide 128-bit security for the ordinary discrete logarithm problem, it suffices to have an elliptic curve with group size approximately 2^256. The security of the digital signatures in the Bitcoin network are based on the intractability of solving the discrete logarithm problem on a particular elliptic curve (called secp256k1) of approximately this size.
Unfortunately, there is no easy way to bijectively map the points of this elliptic curve to an interval of the correct size. It was possible with the previous group, Construction I, thanks to the fact that the multiplicative subgroup of is exactly the interval {1, 2, 3, …, q − 1}, and that can be mapped to the standard interval {0, 1, 2, …, q − 2} by subtracting 1. But the same thing cannot be done for elliptic curves because the usual way of representing points (x, y) as the pair of the x-coordinate and the sign of y is not bijective: roughly half of the numbers in {0, 1, …, p − 1, ∞} cannot occur as valid values of x because the corresponding values of x³ + ax + b are quadratic nonresidues (so cannot equal y²).
There is a class of elliptic curves for which we can efficiently biject the points with an interval, namely supersingular elliptic curves, but unfortunately this just ends up as a disguised version of Construction I: the elliptic curve discrete logarithm problem for these curves is reducible to discrete logarithm modulo p.
Construction II: twists to the rescue!
If d is a quadratic nonresidue, then the following pair of elliptic curves:
- E: y² = x³ + ax + b;
- E‘: y² = d(x³ + ax + b);
are known as quadratic twists of each other. The values of x which lie on E‘ precisely fill in the ‘holes’ formed by the values of x which don’t lie on E, because d(x³ + ax + b) is a quadratic residue precisely when x³ + ax + b is not! (Some extra care is needed to handle the points where y² is 0 or ∞.)
Specifically, we have:
|E| + |E‘| = 2p + 2
and, importantly, we have an explicit bijection between [2p + 2] and the union of the two elliptic curves. As such, if E and E‘ are both cyclic groups and have intractable discrete logarithm problems, then we can manufacture a one-way permutation on [2p + 2] as I describe in this StackExchange answer. This construction appears to have been discovered in 1991 by Burton S. Kaliski Jr.
Avoiding small cycles
Let’s suppose we want to use this one-way bijection inside a pseudorandom number generator, similar to Blum-Blum-Shub but without the existence of a trapdoor (the factorisation of M = pq). It is entirely plausible that φ contains fixed points or short cycles, which would result in periodic output from the pseudorandom number generator.
In particular, if we apply Construction II to a pair of curves with p = 2^255 − 19, we obtain a one-way permutation on [2^256 − 36]. For convenience, we can pad this to a permutation on [2^256] by extending it with the identity function on the remaining 36 points. This permutation has at least 36 fixed points, and plausibly a few more than that.
We’ll extend this to a one-way permutation on [2^384] as follows:
Split the input into a 256-bit ‘upper part’ and a 128-bit ‘lower part’. Apply the one-way permutation to the upper part, and apply a period-2^128 permutation (such as an appropriate affine function modulo 2^128) to the lower part. Then XOR the lower part into the upper part, in-place, to ‘perturb’ it.
By looking at the lower part in isolation, we know that this permutation does not have any cycles of length shorter than 2^128. Moreover, the interaction from the lower part to the upper part is designed to ensure that every orbit will benefit from the hardness of the elliptic curve discrete logarithm problem; without it, the 36 trivial fixed points of the permutation on [2^256] would each give rise to a weak random number generator (a 128-bit LCG).
To use this as an actual cryptographic random number generator, you’d need to choose a suitable output function — for instance, taking a RIPEMD-160 hash* of the 384-bit internal state — and then be careful** to implement the whole thing using constant-time instructions to avoid timing attacks. (On most CPUs, for example, the multiplication instruction lacks this property.)
*practical cryptographic random number generators such as ChaCha20 use less computationally intensive output functions, but in this case we don’t care because it still pales in comparison to the amount of computation in the state update function.
**harder than it seems, because the compiler may optimise your constant-time code into faster variable-time code. Unless you absolutely need the property that its previous internal states cannot be deduced from its current internal state, then I’d recommend using a well-tested implementation of ChaCha20 instead of this 384-bit PRNG.